а)Первый способ. Вычисление поверхностного интеграла (13.1) сводится к вычислению двойных интегралов по тем областям, которые получаются при проецировании поверхности 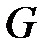 на координатные плоскости.
на координатные плоскости.
Пусть функция  непрерывна во всех точках гладкой поверхности
непрерывна во всех точках гладкой поверхности  которая однозначно проецируется на координатную плоскость
которая однозначно проецируется на координатную плоскость  в область
в область  и её уравнение можно представить в виде
и её уравнение можно представить в виде 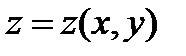 . Ориентируем поверхность так, что нормальный к ней вектор составляет острый угол
. Ориентируем поверхность так, что нормальный к ней вектор составляет острый угол  с осью
с осью  . Интегральная сумма, приводящаяся к поверхностному интегралу, в этом случае будет выглядеть следующим образом:
. Интегральная сумма, приводящаяся к поверхностному интегралу, в этом случае будет выглядеть следующим образом:  .
.
В пределе при соответствующих условиях получим преобразование поверхностного интеграла 2-ого рода по переменным  и
и  в двойной:
в двойной:
 .
.
Если выбрать другую ориентацию поверхности, тогда вектор нормали будет составлять с осью  тупой угол и перед двойным интегралом появится знак «минус».
тупой угол и перед двойным интегралом появится знак «минус».
Аналогично для непрерывных функций 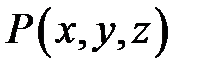 и
и 
 , где
, где  - уравнение поверхности
- уравнение поверхности  и нормальный вектор составляет с осью
и нормальный вектор составляет с осью 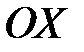 острый угол
острый угол  , и
, и  , где
, где  - уравнение поверхности
- уравнение поверхности  и нормальный вектор составляет с осью
и нормальный вектор составляет с осью  острый угол
острый угол  .
.
В общем случае поверхностный интеграл 2-ого рода по гладкой ограниченной поверхности, которая однозначно проецируется в каждую из координатных плоскостей, сводится к трём двойным интегралам, знаки перед которыми выбираются соответственно тому, какие углы составляет выбранный нормальный вектор с осями координат.
 .(13.2)
.(13.2)
Пример 13.1. Вычислим интеграл  , где
, где  - часть поверхности
- часть поверхности  ограниченная так, что
ограниченная так, что  , если вектор нормали к поверхности составляет острый угол с положительным направлением оси OX.
, если вектор нормали к поверхности составляет острый угол с положительным направлением оси OX.
Решение. Построим часть цилиндра параболического, ограниченную заданными плоскостями (см. рис. 13.3)
| Рисунок 13.3 |
 По рисунку видим, что вектор
По рисунку видим, что вектор 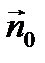 составляет с осью OX острый угол, с OY - прямой, с OZ – тупой, следовательно,
составляет с осью OX острый угол, с OY - прямой, с OZ – тупой, следовательно, | Рисунок 18.3 |
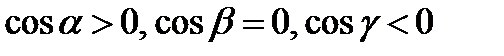 . Следовательно, часть интеграла по переменным
. Следовательно, часть интеграла по переменным  и
и  должна быть взята со знаком «плюс», часть по
должна быть взята со знаком «плюс», часть по  и
и  обратиться в ноль, а часть по
обратиться в ноль, а часть по  и
и  следует
следует взять со знаком «минус». 




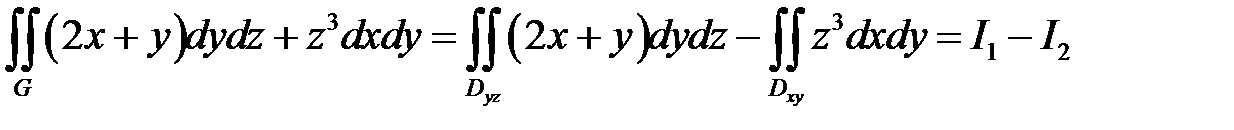 .
.
Вычислим  . Для этого построим проекцию области
. Для этого построим проекцию области  на плоскость
на плоскость  .
.  Уравнение проекция линии пересечения
Уравнение проекция линии пересечения  и
и  на плоскость YOZ:
на плоскость YOZ:  .
.
Из уравнения поверхности  выразим переменную
выразим переменную  и, подставив в подынтегральное выражение, вычислим интеграл.
и, подставив в подынтегральное выражение, вычислим интеграл.
 .
.
Вычислим 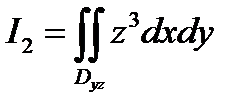 . Для этого построим проекцию области
. Для этого построим проекцию области  на плоскость
на плоскость  . Переменную
. Переменную  из уравнения поверхности
из уравнения поверхности  подставим в подынтегральное выражение и вычислим интеграл.
подставим в подынтегральное выражение и вычислим интеграл.
 . Ответ:
. Ответ:  .
.
б)Второй способ вычисления поверхностного интеграла 2-ого рода.
Заметим, что если 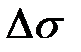 - площадь элементарной части поверхности
- площадь элементарной части поверхности  и нормальный вектор к этой площадке составляет с осями координат углы
и нормальный вектор к этой площадке составляет с осями координат углы 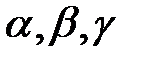 , то
, то 
 . И тогда
. И тогда
 . (13.3)
. (13.3)
То есть поверхностный интеграл 2-ого рода сводится к поверхностному интегралу 1-ого рода. (см. занятие 12)
Отметим, что если уравнение поверхности  имеет вид
имеет вид  , то единичный нормальный вектор к ней в точке
, то единичный нормальный вектор к ней в точке 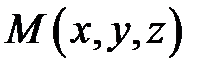 имеет координаты, совпадающие с его направляющими косинусами
имеет координаты, совпадающие с его направляющими косинусами
 ,
,  ,
,  . (13.4)
. (13.4)
Подставив эти выражения в подынтегральное выражение и упростив его, получим интеграл вида  .
.
Таким образом поверхностный интеграл 2-ого рода сведём к поверхностному интегралу 1-ого рода. (см. занятие 12).
Пример 13.2. Вычислим интеграл  в условиях примера 13.1, преобразовав его в поверхностный интеграл 1-ого рода (см. (13.3) и (13.4)). Для этого найдём направляющие косинусы единичного нормального вектора к поверхности.
в условиях примера 13.1, преобразовав его в поверхностный интеграл 1-ого рода (см. (13.3) и (13.4)). Для этого найдём направляющие косинусы единичного нормального вектора к поверхности.
В рассматриваемом примере уравнение поверхности имеет вид 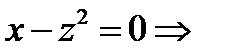
 и тогда
и тогда 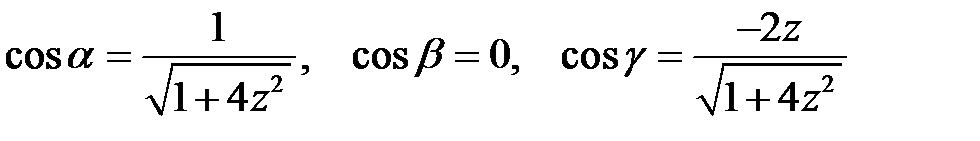 с учётом того, что нормальный вектор составляет острый угол с осью OX. Преобразуем данный интеграл в поверхностный 1-ого рода.
с учётом того, что нормальный вектор составляет острый угол с осью OX. Преобразуем данный интеграл в поверхностный 1-ого рода.

 .
.
Для вычисления получившегося поверхностного интеграла I рода спроецируем σ на плоскость XOY (см. рис. 13.3) и преобразуем интеграл в двойной (см. (12.1): 
Из уравнения поверхности 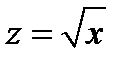 следует, что:
следует, что: 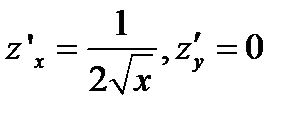 , и
, и  .
.
Подставим всё в подынтегральное выражение, расставим пределы интегрирования в повторном интеграле и вычислим его.
Получаем  .
.
Ответ:  .
.
Занятие 14.
Векторное поле (определение). Векторные линии поля и их дифференциальные уравнения. Определение потока векторного поля через поверхность и дивергенция векторного поля. Теорема Остроградского-Гаусса для односвязной области. Физический смысл дивергенции. Стоки и источники поля. Соленоидальное векторное поле и его свойства.
ОЛ-1 гл.6,7, ОЛ-2 гл.3, ОЛ-4 § 12, п. 12-3.
Практика: ОЛ-6 №№ 2374, 2361, 2365, 2367 или ОЛ-5 №№ 10.95, 102, 103, 105, 108, 145.
Домашнее задание к занятию 14: ОЛ-6 №№ 2362, 2364, 2366, 2368 или ОЛ-5 №№ 10.96, 99, 104, 144, 146.
Векторное поле.
Определение. Если каждой точке  некоторой области
некоторой области  поставлен в соответствие по некоторому правилу (закону) вектор
поставлен в соответствие по некоторому правилу (закону) вектор  , то множество этих векторов называется векторным полем.
, то множество этих векторов называется векторным полем.
Задание векторного поля адекватно заданию вектор -функции  с областью определения G. Если G - область трёхмерного пространства
с областью определения G. Если G - область трёхмерного пространства  с введённой в ней декартовой системой координат
с введённой в ней декартовой системой координат 
 с ортами
с ортами  , направленными по осям, то задание векторного поля равносильно заданию трёх скалярных функций-координат, каждая из которых зависит от трёх переменных:
, направленными по осям, то задание векторного поля равносильно заданию трёх скалярных функций-координат, каждая из которых зависит от трёх переменных:  .
.
Если G - область на плоскости  , то в декартовых координатах скалярное поле задаётся функцией двух переменных
, то в декартовых координатах скалярное поле задаётся функцией двух переменных  , а векторное поле – двумя функциями двух переменных
, а векторное поле – двумя функциями двух переменных  . В этом случае поле называется плоским.
. В этом случае поле называется плоским.
Физические примеры векторных полей: электрическое поле системы электрических зарядов, характеризующееся в каждой точке вектором напряжённости электрического поля 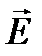 ; магнитное поле, создаваемое электрическим током и характеризующееся в каждой точке
; магнитное поле, создаваемое электрическим током и характеризующееся в каждой точке  вектором магнитной индукции
вектором магнитной индукции  ; поле скоростей потока движущейся жидкости, описываемое в каждой точке вектором скорости
; поле скоростей потока движущейся жидкости, описываемое в каждой точке вектором скорости 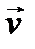 .
.
Поле  называется дифференцируемым n раз, если функции
называется дифференцируемым n раз, если функции 
дифференцируемы n раз. В дальнейшем будем считать, что рассматриваемое поле дифференцируемо нужное нам число раз.
Определение. Действительная функция  , определённая в каждой точке
, определённая в каждой точке  некоторой области
некоторой области  , называется скалярным полем
, называется скалярным полем  .
.
 2017-11-01
2017-11-01 2633
2633