Предмет теории вероятностей. Классификация событий. Операции над событиями. Алгебра событий

M 1.Элементы комбинаторики. Правила сложения и умножения.

Комбинаторика- раздел математики, который изучает способы подсчета числа элементов различных множеств.

Выборкой из n-элементов длинной в k- элементов называется отбор k-элементов из общей совокупности n-элементов.

БЕЗ ПОВТОРА ЭЛЕМЕНТОВ	С ПОВТОРОМ ЭЛЕМЕНТОВ
1. Перестановками, без повторения элементов называются выборки из n-элементов длинной в n-элементов без повторений и с учетом порядка. Pn=n! n!=1*2*3…*n (1!=1; 0!=1) Все эл-ты	1. Перестановки с повторением и с учетом порядка. ,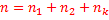
2. Размещение без повторений назыв.выборки из элементов длинной в k-элементов без повторений и с учетом порядка. Часть эл-в	2. Размещение (с повторением элементов). Важен порядок! М.Б. k>n
3. Сочетаниями без повторения назыв. выборки из n- элементов длинной в k-элементов без повторения и без учета порядка.	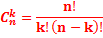3. Сочетание (с повторением элементов). НЕ важен порядок. М.Б. k>n

Правила сложения: если первый элемент можно выбрать - способами, второй - способ и тд. k-ый элемент - способами, то хотя бы 1 элемент м\б выбран (ИЛИ).

Правило умножения: если 1-ый элемент можно выбрать - способами, второй - способ и тд. k-ый элемент - способами, то все k- элементы одновременно можно выбрать. (И).

Предмет теории вероятностей. Классификация событий. Операции над событиями. Алгебра событий.

Раздел математики изучающий случайные процессы и вероятности их наступления.

Опытом назыв. всякое действие, которое происходит неограниченное число раз при неизменном комплексе условий.

Событием называется результат опыта (А, В, С).

Невозможным называют событие которое заведомо не произойдет.

Достоверное называют событие которое может произойти или не произойти.

Суммой событий А и В назыв. событие с заключающийся в наступлении хотя бы одного из событий А и В.

Произведением событий А и В назыв. событие С, заключающееся в одновременном наступлении события А и В.

Разностью события А и В назыв. событие С, заключающееся в том, что А наступит, а В- нет.

Событие назыв. Противоположным к событию А и заключ. в том, что событие А- не наступит.

События А и В назыв. несовместными если, появление одного из них в результате испытания исключает появление другого.

События А и В назыв. независимыми, если вероятность появления одного из них не меняется при наступлении другого события.

События образуют полную группу событий, если они попарно не совместны и одно из них является событием достоверным.