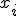 | ||||
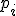 | 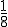 | 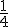 | 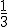 |  |
Найти: 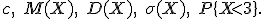
1) Так как 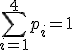 , т.е.
, т.е. 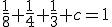 , следовательно
, следовательно
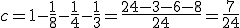
Т.о. закон распределения примет вид
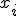 | ||||
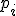 | 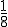 | 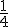 | 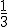 | 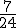 |
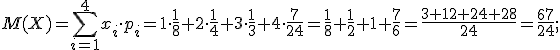
2) Для вычисления дисперсии воспользуемся формулой:
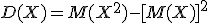
Сначала найдем математическое ожидание ДСВ Х2 для этого составим закон распределения этой СВ. Напоминаю, что для этого необходимо каждое значение ДСВ Х возвести в квадрат, а вероятности оставляем прежними. При одинаковых значениях ДСВ вероятности складываем.
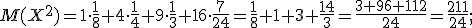
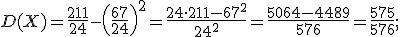
3) Найдем среднее квадратическое отклонение:
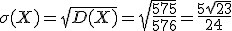
4) 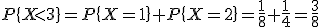
Функция распределения ДСВ Х имеет вид
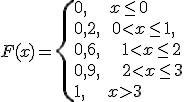
Найти: 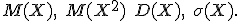
Решение.
Составляем закон распределения ДСВ Х (т.е. выполняем операцию обратную той, которую мы делали в предыдущей статье)
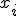 | ||||
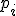 | 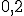 | 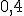 | 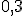 |  |
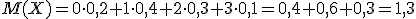
Составляем закон распределения ДСВ Х2
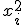 | ||||
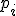 | 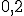 | 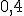 | 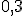 | 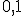 |
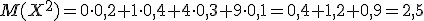
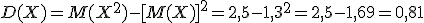
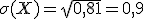
5. Независимые случайные величины X и Y заданы таблицами распределения вероятностей
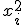 | ||
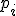 | 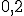 | 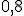 |
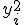 | |||
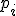 | 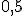 | 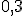 | 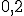 |
Найти 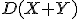 двумя способами:
двумя способами:
1. Составив предварительно таблицу распределения СВ 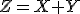 ;
;
Используя правило сложения дисперсий.
Решение.
Составим таблицу распределения ДСВ 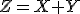 .
.
Найдем 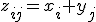
| 10+30=40 | 20+30=50 |
| 10+40=50 | 20+40=60 |
| 10+50=60 | 20+50=70 |
Т.о. значения ДСВ Z таковы: 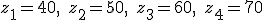
Найдем соответствующие им вероятности:
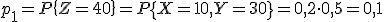
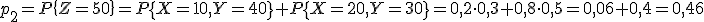
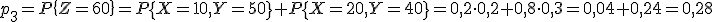
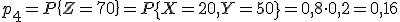
Получаем ряд распределения СВ Z
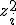 | ||||
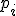 | 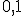 | 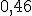 | 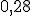 | 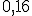 |
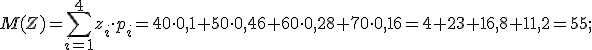
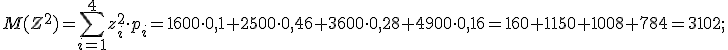
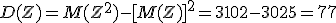
2. Используя правило сложения дисперсий: 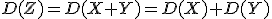
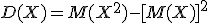
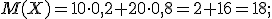
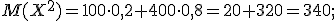
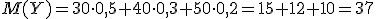
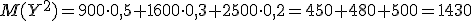
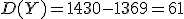
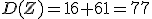
 2017-11-01
2017-11-01 4677
4677