2017-11-01
1151
Как указывалось ранее, точное решение дифференциального уравнения теплопроводности (1.22) удается получить лишь для немногих частных случаев. Поэтому на практике применяются различные приближенные модели решений. Численные методы описания тепловых процессов находят все более широкое применение в связи с развитием вычислительной техники.
Наибольшее распространение в решениях получили модели, основанные на методе сеток. Сущность метода заключается в том, что исследуемая непрерывная функция заменяется совокупностью приближенных значений, рассчитанных в некоторых точках-узлах. Совокупность узлов, соединенных определенным образом, образует сетку. Сетка является дискретной моделью исследуемой непрерывной функции.
Применение метода сеток позволяет свести решение задачи к решению системы алгебраических уравнений, что легко осуществляется на ЭВМ. При решении теплофизических задач наибольшее применение получили следующие виды метода сеток – метод конечных разностей (МКР), метод конечных элементов (МКЭ), метод граничных элементов (МГЭ).
|
|
|
Метод конечных разностей (МКР). Предусматривает разбиение области определения функции на отдельные равные элементы. Рассмотрим, например, распределение температуры вдоль стержня малого сечения (рис.3.4.)
Рис. 3.4 – Использование метода конечных разностей для расчета температурного поля в стержне
Температурное поле в таком стержне будет одномерным (см.процесс иглофрезерования).
Разделим стержень на n равных элементов размером hх.
Время процесса также разделим на равные промежутки Δτ с нумерацией 1, 2, 3...(k + 1), k, (k – 1),...m, т.е. m промежутков.
Можно доказать, что
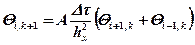. (3.9)
Формула (3.9) выражает дифференциальное уравнение теплопроводности, представленное в конечно-разностной форме. Как видно, это уравнение алгебраическое. Чтобы определить температуру в любой точке тела в данный момент времени (i, k + 1) достаточно знать температуру соседних точек (i+1, i – 1) в предыдущий момент времени (k). Используя граничные начальные условия (они заданы), получаем систему связанных друг с другом уравнений. Таких уравнений будет nm с таким же числом неизвестных. Решая эту систему можно рассчитать температуру в каждой точке твердого тела в любой момент времени. Результат получается тем точнее, чем меньше будут размер элементов hx и промежуток времени Δτ.
Метод конечных элементов (МКЭ). В сложных случаях теплообмена разбиение твердого тела на одинаковые по размеру элементы, а времени – на одинаковые промежутки вызывает большой объем вычислительной работы. В любой конкретной задаче разные участки твердых тел представляют для практики различный интерес. Некоторые объемы твердых тел изучаются с большей степенью детализации (например, температура контактных поверхностей режущих инструментов), чем другие. Метод конечных элементов позволяет осуществлять различную детализацию решения в различных областях изучаемого объекта, причем могут быть использованы элементарные объемы различные не только по величине, но и по конфигурации. Однако решение задачи в этом случае выполняется с использованием вариационного исчисления. При использовании МКЭ число уравнений и число неизвестных может быть значительно меньше, чем при методе конечных разностей, однако математический аппарат существенно сложнее.
|
|
|
Метод граничных элементов (МГЭ)
Существенное отличие МГЭ от МКР и МКЭ состоит в том, что на конечные элементы разбивают только граничные поверхности тела, а не весь его объем. Реализация этого метода приводит к значительным математическим трудностям, поэтому этот метод при анализе тепловых процессов пока применяют значительно редко.
