Лекция 9.2. Дифференциальные уравнения высших порядков
План:
1. Дифференциальные уравнения второго порядка, допускающие понижения порядка.
2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
3. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
На практике достаточно часто сталкиваются необходимостью уметь решать дифференциальные уравнения не первого, а более высокого порядка т.е. дифференциальные уравнения, в которые входят вторая, третья и другие производные искомой функции.
Рассмотрим три типа уравнений второго порядка, допускающих понижение порядка, т.е. позволяющие свести их решение или к интегрированию, или к решению двух дифференциальных уравнений первого порядка.
1. Уравнение вида 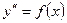 решается последовательным двукратным интегрированием правой части:
решается последовательным двукратным интегрированием правой части:
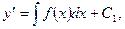
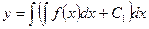 или
или 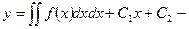
Заметим, что уравнение n -го порядка 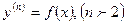 решается последовательным n -кратным интегрированием, понижая на каждом шаге порядок уравнения. Окончательное решение содержит n произвольных постоянных.
решается последовательным n -кратным интегрированием, понижая на каждом шаге порядок уравнения. Окончательное решение содержит n произвольных постоянных.
Пример. Решить уравнение 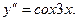
Решение. Последовательно интегрируя два раза данное уравнение, получим
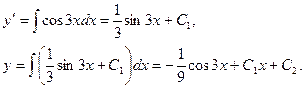
2. Уравнение вида 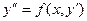 не содержащее явно искомой функции у, подстановкой
не содержащее явно искомой функции у, подстановкой 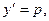 где
где 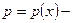 новая неизвестная функция приводится к уравнению первого порядка:
новая неизвестная функция приводится к уравнению первого порядка: 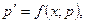 где
где 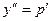 . Решая это уравнение, получаем общее решение в виде
. Решая это уравнение, получаем общее решение в виде 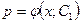 или
или 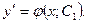 Общее решение уравнения будет иметь вид
Общее решение уравнения будет иметь вид 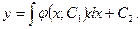
Пример. Решить уравнение 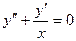 .
.
Решение … Положим 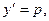 тогда
тогда 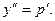 Уравнение перепишется:
Уравнение перепишется:
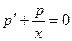 или
или 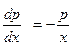 или
или 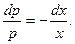
Решим ДУсРП путем интегрирования обеих частей, получим 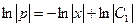 или
или 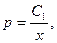 где
где 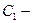 постоянная
постоянная 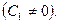
Так как 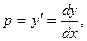 получим:
получим: 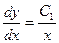 или
или 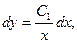
Интегрируя, получим 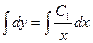 или
или 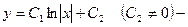 общее решение данного уравнения.
общее решение данного уравнения.
3. Уравнение вида 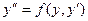 , не содержащее явно независимую переменную х, подстановкой
, не содержащее явно независимую переменную х, подстановкой 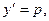 где
где 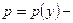 новая неизвестная функция приводится к уравнению
новая неизвестная функция приводится к уравнению 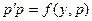 , где
, где 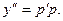 Решая это уравнение, получим общее решение
Решая это уравнение, получим общее решение 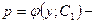 или
или 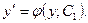 Общее решение уравнения будет иметь вид
Общее решение уравнения будет иметь вид 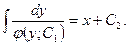
Пример. Решить уравнение 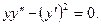
Решение. Положим 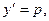 тогда
тогда 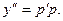 Уравнение перепишется:
Уравнение перепишется:
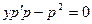 или
или 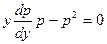 или
или 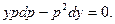
Решим ДУсРП, разделив обе части уравнения на 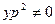 :
:
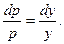
Интегрируя, получим 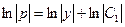 или
или 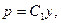 где
где 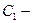 постоянная
постоянная 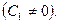
Так как 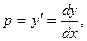 получим:
получим: 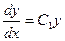 или
или 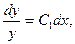
Интегрируя, получим 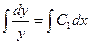 или
или 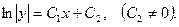 Положим
Положим 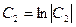 имеем
имеем 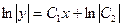 или
или 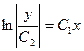 или
или 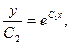 отсюда
отсюда
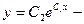 общее решение данного уравнения.
общее решение данного уравнения.
 2014-01-25
2014-01-25 1016
1016
