Линейным дифференциальным уравнением второго порядка называется уравнение вида:
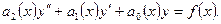
Если 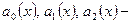 постоянные числа, то уравнение будем называть уравнением с постоянными коэффициентами. Кроме этого, будем считать что коэффициент при второй производной равен 1. Положим
постоянные числа, то уравнение будем называть уравнением с постоянными коэффициентами. Кроме этого, будем считать что коэффициент при второй производной равен 1. Положим 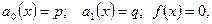 где
где 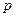 и
и 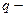 произвольные числа.
произвольные числа.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами (ЛОДУ) называется уравнение вида
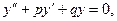
где 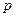 и
и 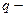 некоторые действительные числа.
некоторые действительные числа.
Общее решение ЛОДУ находится достаточно просто, если известны, так называемые, линейно независимые частные решения этого уравнения.
Функции 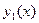 и
и 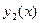 называются линейно независимыми на множестве D, если их отношение не является постоянной величиной, то есть
называются линейно независимыми на множестве D, если их отношение не является постоянной величиной, то есть 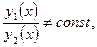 или другими словами: не существует такого постоянного числа
или другими словами: не существует такого постоянного числа 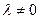 при котором выполнено равенство
при котором выполнено равенство 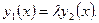
В противном случае, функции 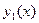 и
и 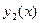 называются линейно зависимыми. Например, функции
называются линейно зависимыми. Например, функции 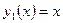 и
и 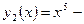 линейно независимые, а функции
линейно независимые, а функции 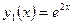 и
и 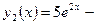 линейно зависимые.
линейно зависимые.
Обозначим через 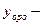 общее решение однородного уравнения ().
общее решение однородного уравнения ().
Теорема 8.4. (о структуре общего решения ЛОДУ второго порядка). Если 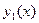 и
и 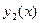 – два линейно независимые частные решения ЛОДУ
– два линейно независимые частные решения ЛОДУ 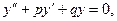 то функция
то функция 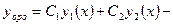 общее решение этого уравнения, где
общее решение этого уравнения, где 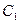 и
и 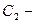 произвольные постоянные.
произвольные постоянные.
Замечание: Не существует общего метода нахождения частных решений уравнения 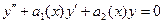 , когда коэффициент
, когда коэффициент 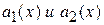 переменные, но для случая, когда они являются константами, Эйлером создан очень удобный метод нахождения частных решений.
переменные, но для случая, когда они являются константами, Эйлером создан очень удобный метод нахождения частных решений.
Характеристические уравнения для ЛОДУ второго порядка:
Будем искать решение 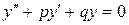 в виде
в виде 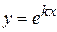 , где k-const.
, где k-const.
Очевидно, что 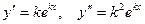 . Подставим эти выражения в уравнение:
. Подставим эти выражения в уравнение:
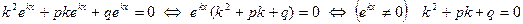
Уравнение 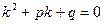 называется характеристическим уравнением дифференциального уравнения
называется характеристическим уравнением дифференциального уравнения 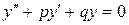 .
.
Характеристическое уравнение 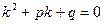 есть алгебраическое квадратное уравнение, имеющее два корня
есть алгебраическое квадратное уравнение, имеющее два корня 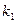 и
и 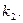 Эти корни, в зависимости от дискриминанта, могут быть действительными и не равными друг другу, действительными и равными и комплексно-сопряженными.
Эти корни, в зависимости от дискриминанта, могут быть действительными и не равными друг другу, действительными и равными и комплексно-сопряженными.
1. 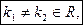 т.е корни действительные и не равные друг другу.
т.е корни действительные и не равные друг другу.
По теореме общее решение ЛОДУ второго порядка имеет вид:
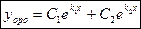
2. 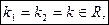 т.е корни действительные и равные друг другу.
т.е корни действительные и равные друг другу.
По теореме общее решение ЛОДУ второго порядка имеет вид:
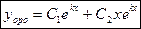 или
или 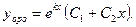
3. 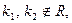 т.е корни комплексно сопряженные числа:
т.е корни комплексно сопряженные числа: 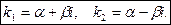
По теореме общее решение ЛОДУ второго порядка имеет вид:
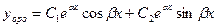 или
или 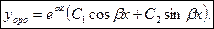
Пример. Найти общее решение ЛОДУ второго порядка:
а) 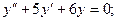 б)
б) 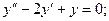 в)
в) 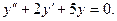
Решение. а) Составим характеристическое уравнение для данного ЛОДУ: 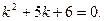 Найдем корни квадратного уравнения
Найдем корни квадратного уравнения 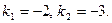 Корни действительные и не равные друг другу. Следовательно, общее решение ЛОДУ имеет вид:
Корни действительные и не равные друг другу. Следовательно, общее решение ЛОДУ имеет вид: 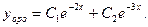
б) Составим характеристическое уравнение для данного ЛОДУ: 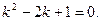 Найдем корни квадратного уравнения
Найдем корни квадратного уравнения 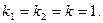 Корни действительные и равные друг другу. Следовательно, общее решение ЛОДУ имеет вид:
Корни действительные и равные друг другу. Следовательно, общее решение ЛОДУ имеет вид: 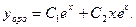
в) Составим характеристическое уравнение для данного ЛОДУ: 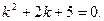 Найдем корни квадратного уравнения
Найдем корни квадратного уравнения 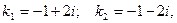 где
где 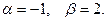 Корни комплексные и сопряженные. Следовательно, общее решение ЛОДУ имеет вид:
Корни комплексные и сопряженные. Следовательно, общее решение ЛОДУ имеет вид: 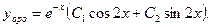
Пример.. Найти частное решение уравнения, удовлетворяющее заданному начальному условию 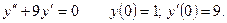
Решение. Составим характеристическое уравнение: 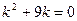 или
или 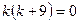 или
или 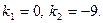 Следовательно, общее решение ЛОДУ имеет вид:
Следовательно, общее решение ЛОДУ имеет вид: 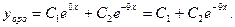
Найдем частное решение, путем вычисления 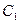 и
и 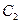 из системы
из системы 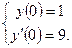
Найдем 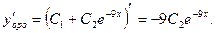 Подставим в
Подставим в 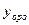 и
и 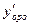
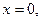 получим
получим
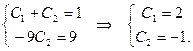 Тогда частное решение примет вид:
Тогда частное решение примет вид: 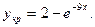
 2014-01-25
2014-01-25 1667
1667
