Линейная функция 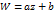
Отображение 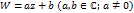 будет конформным во всей плоскости
будет конформным во всей плоскости 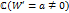
Функция 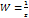
Соответствие, даваемое этой формулой, взаимнооднозначно во всех точках плоскости, причем в нулевой точке z=0 (W=0) соответствует бесконечно удаленная точка W=∞ (z=0)
Полагая 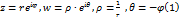
Рассмотрим окружность 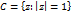
Преобразовав (1) удобно разбить на 2 более простых
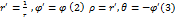 .
.
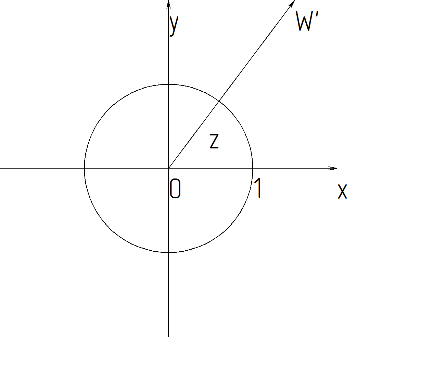 При преобразовании (2) аргумент сохраняется, а модуль изменяется на обратный. Точка z, находящаяся внутри окрестности C, преобразуется в точку W’, находящуюся вне окружности и лежащую на продолжении отрезка Oz,причем расстояние между 0, z и W’ равно 1.
При преобразовании (2) аргумент сохраняется, а модуль изменяется на обратный. Точка z, находящаяся внутри окрестности C, преобразуется в точку W’, находящуюся вне окружности и лежащую на продолжении отрезка Oz,причем расстояние между 0, z и W’ равно 1.
Такое отображение называется инверсией относительно окрестности C. Точки z и W’ при этом называются взаимно симметричными относительно окрестности C.
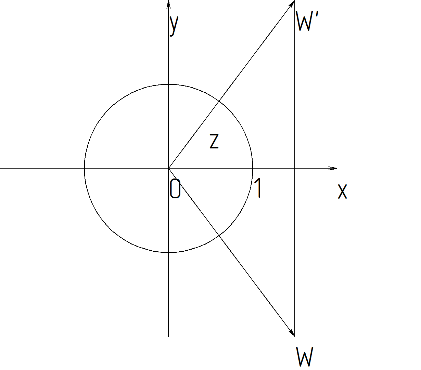 Отображение (2) можно записать в виде:
Отображение (2) можно записать в виде: 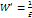
Преобразовав (3): 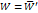
Совокупность двух отображений дает голоморфное (z≠0) отображение 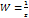
Это отображение будет сохранять углы во всех плоскостях  , включая z=0, z=∞
, включая z=0, z=∞
При этом под углом двух линий при z=∞ понимают угол, образованныйотображениием линиями посредством функции 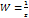 в плоскости W при W=0.
в плоскости W при W=0.
Дробно-линейная функция 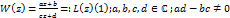
Обратно, z можно выразить через W: 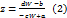
Таким образом, соответсвуют формулы (1) является взаимно однозначным
точка 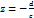 будет соответствовать W=∞, а точка
будет соответствовать W=∞, а точка 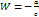 - точка z=∞.
- точка z=∞.
Функция (1) сохраняет углы во всех точках расширенной плоскости 
Теор: Образом прямой или окружности при отображении 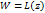 является прямая или окружность.
является прямая или окружность.
Док-во: Для линейной функции 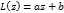 это свойство является очевидным.
это свойство является очевидным.
Расссмотрим отображение 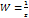 . Уравнение окружности имеет вид:
. Уравнение окружности имеет вид:  .
.
При A=0 уравнение (3) определяет прямую.
Перепишем это уравнение в виде:
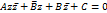 , где AиC – действительные постоянные,
, где AиC – действительные постоянные, 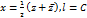
При преобразовании 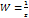 получаем
получаем 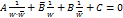 , или приведя к общему знаменателю, находим
, или приведя к общему знаменателю, находим 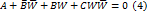
Уравнение (4) определяет окружность плоскости W (приC=0 оно предстанляет прямую)
Поскольку преобразование 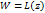 представляет собой комбинацию преобразований, для которых круговое свойство выполняется, то теорема доказана.
представляет собой комбинацию преобразований, для которых круговое свойство выполняется, то теорема доказана.
Круговое свойство дробно-линейного отображения, свойство сохранения симметрии, инвариантность ангармонического отношения.
Дробно-линейное отображение 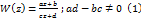
Зависит от трех параметров, за которые могут принять, например, отношение чисел a, b, c, d к одному из них.
Эти параметры однозначно определяется из требований, чтобы три заданных точки z1, z2, z3 плоскости 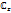 переходит в заданные точки W1, W2, W3 плоскости
переходит в заданные точки W1, W2, W3 плоскости 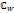 :
: 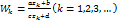
Чтобы исключить a, b, c, d из этих уравнений и из уравнения 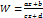 образуем разности:
образуем разности:
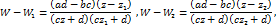
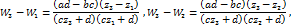 Отсюда получим
Отсюда получим
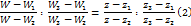
Теор1: При невырожденном дробно-линейном отображении (1) с действительными коэффицентами верхняя полуплоскость ImZ>0 переходит в верхнюю полуплоскость ImW>0, если ad-bc>0 и нижнюю, если ad-bc<0
Опр: Выражение 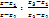 называется двойным. Равенство (2) означает инвариантность ангармонического отношения четырех точек при невырожденном дробно-линейном отображением
называется двойным. Равенство (2) означает инвариантность ангармонического отношения четырех точек при невырожденном дробно-линейном отображением
Теор2: (свойство сохранения симметрии) Если точки z1,z2 симметричны относительно некоторой прямой или окружности при дробно-линейном отображении 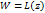 их образы будут симметричны относительно образов γ:
их образы будут симметричны относительно образов γ: 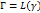
8. Степенная функция W = Zn. Риманова поверхность функции Z= 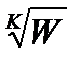 .
.
ФункцияW=Zn однозначна и непрерывана на всей плоскости 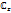 . При n=1 она тождественно отображает
. При n=1 она тождественно отображает 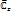 на
на 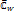 . При отображении W=Znкаждый луч
. При отображении W=Znкаждый луч 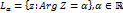 переводит в луч
переводит в луч 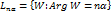 и, следовательно, углы с вершиной в точке z=0 увеличиваются в n раз. Точки z1,z2, у которых модули равны, а аргументы отличаются на величину, кратную 2π/nотображающ в одну точку, в силу чего Zn (n≥2) в
и, следовательно, углы с вершиной в точке z=0 увеличиваются в n раз. Точки z1,z2, у которых модули равны, а аргументы отличаются на величину, кратную 2π/nотображающ в одну точку, в силу чего Zn (n≥2) в 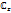 неоднолистна.
неоднолистна.
Однако на каждом множестве, не содержащих равных по модулю точек, с равными по модулю 2π/n аргументами, функция Znоднолистна.
Примерами таких множеств служат углы 
В частности 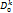 исключив из него луч
исключив из него луч 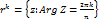 , получив область
, получив область 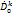 , которая однолистно отображается функцией Zn на область
, которая однолистно отображается функцией Zn на область 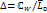
В этой области однозначной является функция 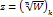 – ветви функции
– ветви функции 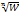 – обратной к функции W=Zn и называемой корнем n -ной степени.
– обратной к функции W=Zn и называемой корнем n -ной степени.
В области ∆ она является аналитической функцией, причем 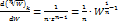
Значение 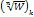 при
при 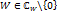 принадлежат
принадлежат 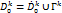
Пусть 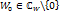 и значение
и значение 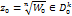
Переместим точку W от W0 по окружности | W |=| W0 |, описывая при этом полную окружность. Тогда ArgW непрерывно возрастет на 2π, а 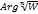 возрастет на 2π/n ⇒после обхода окрестности переходим к значению
возрастет на 2π/n ⇒после обхода окрестности переходим к значению 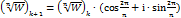 После n -кратного обхода окрестности в одном направлении получим
После n -кратного обхода окрестности в одном направлении получим 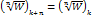 , т.е. указанные ветви функции
, т.е. указанные ветви функции 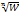 совпадают.
совпадают.
Рассмотрим n экземпляров области 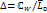 , которые обозначим ∆0,∆1, …, ∆n-1Наложим эти области одна на другую и склеим нижний край разреза
, которые обозначим ∆0,∆1, …, ∆n-1Наложим эти области одна на другую и склеим нижний край разреза  листа ∆k (k=0,1,2,…,n-2)с верхним краем такого же разреза листа ∆k+1 Свободный верхний край разреза L0 листа ∆0 склеим с нижним краем разреза ∆n+1
листа ∆k (k=0,1,2,…,n-2)с верхним краем такого же разреза листа ∆k+1 Свободный верхний край разреза L0 листа ∆0 склеим с нижним краем разреза ∆n+1
Если точка М – внутренняя для листа ∆k (∆k+1), то у нее существует ε окрестность, принадлежащяя тому же листу, если М лежит на линии склеивания ∆k с ∆k+1, то ε окрестность точки М составленная из части ее ε окрестности, принадлежащей ∆k и распространяющ на нижнюю полуплоскость, из части ε окрестности, принадлежащей ∆k+1 и рапространяющ в верхнюю полуплоскость, а также из ε интервалов, лежащих на L0 и симметрично относительно М построенная n -листная область называется Римановой поверхностью функции 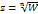
9. Экспоненциальная функция еz. Риманова поверхность функции Z = Ln(W)
Из равенства 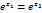 следует, что
следует, что 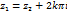 , так что областью однолистности
, так что областью однолистности 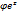 является любая полоса шириной
является любая полоса шириной 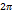 действительной оси. Разделим плоскость (z) на совокупность полос
действительной оси. Разделим плоскость (z) на совокупность полос  При отображении W=ez полосе
При отображении W=ez полосе 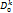 соответствует вся плоскость! с удаленной из нее точкой W=0. Открытая часть полосы
соответствует вся плоскость! с удаленной из нее точкой W=0. Открытая часть полосы 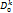 , т.е. области
, т.е. области 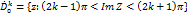 отображ на
отображ на 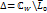 где L 0 – отрицательная и действительная оси,
где L 0 – отрицательная и действительная оси, 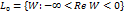 А прямые
А прямые 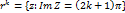 отображ на L 0
отображ на L 0
Из равенства  Отсюда
Отсюда 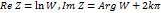 , следовательно все значения функции LnW, обратной к функции W=ezдля
, следовательно все значения функции LnW, обратной к функции W=ezдля 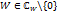 определяется по формуле:
определяется по формуле: 
В областьи∆ имеем счетное множество однозначных ветвей LnkW 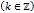 функцииLnW, каждый из которых отображает ∆ на
функцииLnW, каждый из которых отображает ∆ на 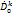 В точке W=1 ветвь LnkWпринимает значение
В точке W=1 ветвь LnkWпринимает значение 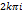 ; оно может быть использовано для выделения
; оно может быть использовано для выделения 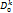 среди всех других рассматриваемых полос. Пусть
среди всех других рассматриваемых полос. Пусть 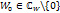 и фиксировано, а z0 – значение LnW, принадлежащее
и фиксировано, а z0 – значение LnW, принадлежащее 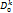 Переместим точку Wот точки W0по окрестности|W|=|W0| против часовой стрелелки до той же точки W0При этом ArgWвозрастает на
Переместим точку Wот точки W0по окрестности|W|=|W0| против часовой стрелелки до той же точки W0При этом ArgWвозрастает на 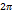 и точке W0будет соответствовать точка
и точке W0будет соответствовать точка 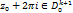 иначе говоря, ветвь LnkWперейдет в ветвь
иначе говоря, ветвь LnkWперейдет в ветвь  с помощью многократного повторения можно перейти от заданной ветви LnkW к другой его ветви.
с помощью многократного повторения можно перейти от заданной ветви LnkW к другой его ветви.
Рассмотри счетное множество областей 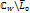 которое обозначим …,∆-2,∆-1,∆0,∆1,∆2,… Будем считать их наложенными друг на друга в порядке возрастания номеров.
которое обозначим …,∆-2,∆-1,∆0,∆1,∆2,… Будем считать их наложенными друг на друга в порядке возрастания номеров.
Склеим верхний край разреза  листа ∆k+1Бесконечнолистная поверхность получающаяся как результат указанных объединений листов ∆k называется Римановой поверхностью функции z=LnW
листа ∆k+1Бесконечнолистная поверхность получающаяся как результат указанных объединений листов ∆k называется Римановой поверхностью функции z=LnW
ФункцияW=ez голоморфно отображается 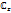 на риманову поверхность функцию z=LnW. Точка W=0 при обходе которой совершается переход с одного лиса на другой называется трансцендентной точкой ветвления функции z=LnW
на риманову поверхность функцию z=LnW. Точка W=0 при обходе которой совершается переход с одного лиса на другой называется трансцендентной точкой ветвления функции z=LnW
10.Интеграл от функции комплексного переменного вдоль кривой. Вычисление интеграла. Интеграл вдоль окружности от функции Zk, k ϵ Z. Свойства интеграла
Опр: число 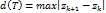 , (
, (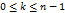 ) наз диаметром разбиения Т кривой Г.
) наз диаметром разбиения Т кривой Г.
Опр: пусть 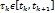 ,
, 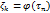 . Сумма
. Сумма 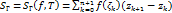 (1) наз-ся инт суммой кривой для фун-ции f на Г, соотв разбиению Т, выбору точек
(1) наз-ся инт суммой кривой для фун-ции f на Г, соотв разбиению Т, выбору точек 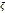 .
.
Опр: ф-ция f наз-ся интегрируемой по кривой Г, если 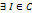 облад след св-вом:
облад след св-вом: 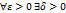 , такое что пр любом разбиении Т крив Г с диаметром
, такое что пр любом разбиении Т крив Г с диаметром 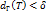 и при каждом выборе точек
и при каждом выборе точек 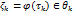 вып нер-во
вып нер-во 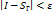 . Число I наз инт от ф-ции f вдоль(или по) кривой Г и обознач
. Число I наз инт от ф-ции f вдоль(или по) кривой Г и обознач 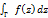 , а Г наз-ся путем интегрирования.
, а Г наз-ся путем интегрирования.
Зам: 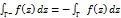
Теор: Если ф-ция f непрер на спрямляемой крив Г, то ф-ция f инт на этой кривой.
Зам: пусть Г-гладкая кривая, 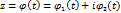 (a<t<b), тогда ее ур-ние
(a<t<b), тогда ее ур-ние 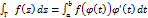
Св-ва инт:
1 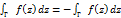
2 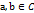
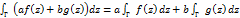
3 если спрямляемая кривая Г состоит из m кусков 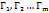 , а ф-ция
, а ф-ция 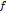 непрер на Г, то ин-л
непрер на Г, то ин-л 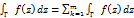 , причем предп, что инт по каждому из
, причем предп, что инт по каждому из 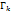 происходит в направлении, порождаемом напр интегр по Г.
происходит в направлении, порождаемом напр интегр по Г.
В случае 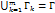 не пересекает спярм крив
не пересекает спярм крив 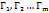 (m≥2) не образуют кривой, ф-лу
(m≥2) не образуют кривой, ф-лу 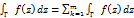 будем считать справедливой по опр.
будем считать справедливой по опр.
4 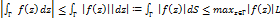 , где L- длина кривой Г
, где L- длина кривой Г
11. Интегральная теорема Коши для жордановой области и для составного контура.
Теор: если ф-ция f голоморфна в односвязной области 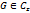 и Г-любая спрямляемая замкнутая кривая, лежащая в
и Г-любая спрямляемая замкнутая кривая, лежащая в  , то
, то 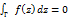
Док-во: все док-во основано на леммах 1 и 2
Лемма 1: пусть f-непрерывна в односвяз области  и для любого треугольника, содерж в Г, ин-л вдоль границы этого тр-ка
и для любого треугольника, содерж в Г, ин-л вдоль границы этого тр-ка 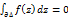 , тогда любой замкнутой спрямляемой кривой Г, содерж в
, тогда любой замкнутой спрямляемой кривой Г, содерж в  ин-л
ин-л 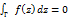
Док-во: основано на том, что любую фигуру(область), можно разбить на тр-ки
Лемма 2: ф-ция f голоморфна в односвязной области 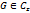 и
и 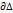 -контур какого-либо
-контур какого-либо 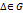 , то
, то 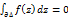
Док-во: любой тр-к можно разбить на последовательность тр-ков, 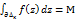 , при достаточно большом к, М устремляется к 0.
, при достаточно большом к, М устремляется к 0.
Пусть Г- жорданова спрямляемая кривая 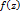 - голоморфна внутри Г, а так же в каждой точке Г. Другими словами, пусть
- голоморфна внутри Г, а так же в каждой точке Г. Другими словами, пусть 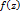 голоморфна в замкнутой области
голоморфна в замкнутой области  кривой Г, в этом случае имеем
кривой Г, в этом случае имеем 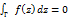
Теор: Пусть граница Г области G состоит из n+1 замкнутых жордановых спрямляемых кривых 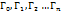 таких, что каждая из прямых
таких, что каждая из прямых 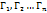 лежит вне остальных и все они располагаются в
лежит вне остальных и все они располагаются в 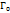 . Пусть при этом если точка движется, то точки области G остаются слева. Тогда если ф
. Пусть при этом если точка движется, то точки области G остаются слева. Тогда если ф 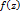 голоморфна в
голоморфна в  , то
, то 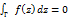 РИС
РИС
Док-во: соединим 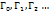 в циклическом порядке с помощью вспомогательных кривых ab,cd,ef.
в циклическом порядке с помощью вспомогательных кривых ab,cd,ef.
Рассмотрим 2 замкнутые кривые 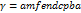 ,
, 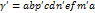
Функция 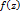 является голоморфной как внутри, так и на каждой из этих кривых
является голоморфной как внутри, так и на каждой из этих кривых  ,
, 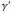
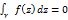 ,
, 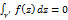
Складывая эти 2 рав-ва получим 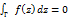 (интегрируя по вспомогательным кривым ab,cd,ef соверш в 2 раза в противопол напр, поэтому уничтожаются)
(интегрируя по вспомогательным кривым ab,cd,ef соверш в 2 раза в противопол напр, поэтому уничтожаются)
Замеч: рав-во 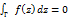 можно записать в виде
можно записать в виде 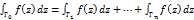 , где интегрирование совершается в положительном направлении кривых
, где интегрирование совершается в положительном направлении кривых 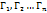
 2018-02-13
2018-02-13 583
583







