Общая постановка задачи

ЛЕКЦИЯ №5

МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

СНУ

Пусть дана система вида:

                                                                        (5.1)

f'(x)=  - производная

Частная производная - вектор (все значения).

 

МЕТОД НЬЮТОНА

Дана система вида (5.1), где f_i один раз непрерывно дифиринцируемые функции, т.е. существуют все частные первые производные этих функций.

Строим последовательность приближений  сходящуюся к точному решению системы .

 Пусть  - некоторое начальное приближение к решению, а - катое приближение к решению. Построим зависимость, позволяющую на основании  построить .

Точное приближение

ξ-корень обращает уравнение в верное равенство(тождество).

                                                        (5.2)

Разложим функции f_i из системы (5.2) в ряд Тейлора в окрестности точки х^к до линейных составляющих.

           (5.3)

Система (5.3) представляет собой систему линейных алгебраических уравнений для поиска компонента вектора поправки h^k.

Перепишем систему (5.3) в виде:

(5.4)

Сокращаем запись системы (5.4):     (5.5)

Решим систему (5.5) методом обратной матрицы. Определитель Якобиана в точке х^к не равен 0.

 

   

Получили связь последующего приближения с предыдущим.

              (5.6)      

условие окончания вычислений. (5.7)

- расстояние между векторами (метрика).

МЕТОД ИТЕРАЦИЙ

Пусть дана система вида (5.1). Преобразуем ее к виду (5.8)

Система (5.8) в векторном виде                                           (5.9)

Необходимо найти неподвижную точку систему

Очевидно, что эта точка ξ – решение системы (5.1)

Пусть дано -некоторое начальное приближение к ξ и на k-том шаге получено приближение . Тогда последующее приближение:

                                  (5.10)

Условие окончания совпадает с (5.7)

Всегда ли метод сходится?

Пусть М- матрица, составлена из элементов m_ij

M=[m_ij], где m_ij=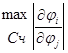

Определение нормы матрицы А: -число удовлетворяющее свойствам.

1) ≥0, =0 ≡0

2) число

3)

4)

Способы задания нормы матрицы:

1) =

2) =

3) =

Достаточное условие сходимости метода итераций:

Если , i=1,n, на Сч и Сч, то процесс итераций сходится независимо от выбора начального приближения.

 

МЕТОД ЗЕЙДЕЛЯ

 

Пусть дана система вида (5.1), преобразуем ее к виду (5.8). Как и в методе итераций строим последовательность приближений  к неподвижной точке.

 

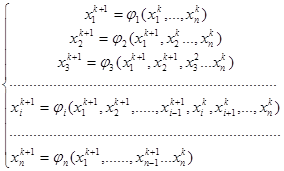
 ускорение сходимости за счет подстановки предыдущего приближения.

Достаточное условие совпадает с достаточными условиями сходимости метода итераций.

Условие окончания получения приближений совпадает с (5.7).

ЛЕКЦИЯ № 6, 7

 

ПРИБЛИЖЕНИЕ ФУНКЦИИ

 

Общая постановка задачи.

Пусть ¦(c) – некоторая функция, которая может быть известно, частично известной и неизвестной. Эту функцию необходимо заменить некоторой «хорошей» функцией j(c), которая будет достаточно близкой ¦(c).