Интерполяционная формула Ньютона дляравноотстоящих узлов

Дана функция y=¦(c),заданная на сетке равноотстоящих узлов:

y_i=¦(c_i), x_i=x₀+ih_i,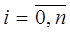

 

Строим интерполяционный полином с целью упрощения записи полинома (интерполяционного) и представления его в виде, позволяющем оценивать влияние каждого из компонентов на значение аппроксимации, запишем его так:

 

N_n(x)=-a₀+a₁(x-x₀)+a₂(x-x₀)(x-x₁)+…+a_n(x-x₀)…(x-x_n-1)                (8.1)

 

Необходимо посчитать его коэффициенты a_i. Будем находить из условия

N_n(x_i)=y_i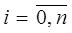  

i=0: N_n(x₀)=y₀=a₀+a₁0+…+a_n0 a₀= y₀

 

i=1: N_n(x₁)=y₁= y₀+a₁(x₁-x₀) + a₂0+…+a_n0

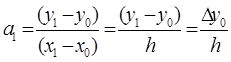
x₁=x₀+1h=x₁-x₀=h

 

i=2: N_n(x₂)=y₂= y₀+∆y₀/h(x₂-x₀) (x₂-x₁) + a₃0+…+a_n0

 

x₂-x₀=2h

x₂-x₁=h

y₂= y₀+∆y₀2+a₂2h²

 

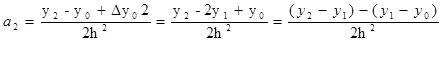
i=k: 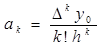                                                            (8.2)

 

Запишем теперь, используя (8.2), полином (8.1) в виде:

 

N_n(x)= y₀+∆y₀/h(x-x₀)+…+ ∆ⁿ y₀ /n!hⁿ(x-x₀)(x-x₁)… (x-x_n-1) (8.3)

 

Полином (8.3) 1-ый интерполяционный многочлен Ньютона. Он наиболее приспособлен для вычисления значения функции в точках, близких к x₀

С целью упрощения записи полинома введем переменную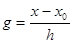

x=x₀+gh

Если g-целое, то будет совпадать с номером узла

x₀ – базовый узел полинома (8.3)

 

x_i=x₀+gh- x₀-ih=h(g-i);

 

N_n(g)= y₀+∆y₀g+…+ ∆ⁿ y₀ /n!g(g-1)(g-2)(g-n+1)                   (8.4)

 

Полином Ньютона в силу единственности существования интерполяционного полинома Лагранжа является одной из форм записи полинома Лагранжа, поэтому для полинома (8.3) справедливо, что формула остаточного члена полинома Лагранжа

 

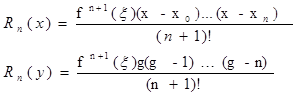
Для вычисления функции в точках находящихся в середине сетки узлов интерполяции либо в ее конце, т. е близкие к x_n, применяют два подхода 

1. строят формулы для вычисления функции в точках х, близких к середине сетки интерполяции

2. формулы для точек х, близких к х_n (упорядочивание узлов интерполяции).

Соответственно получаются формулы Стирлинга, Бесселя, Гаусса, и 2-ой интерполяционный многочлен Ньютона.

Второй путь: в качестве узла х₀ для заданной точки х берут тот узел, который наиболее близок к х, узел х₁ выбирают как самый близкий из оставшихся узлов к х.

Т.е последовательность 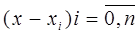упорядочившаяся по возрастанию.

Для вычисления значения функции в точке х используется 1-ый интерполяционный многочлен Ньютона.

 

х0 х1  х2  х3    х4 х5 х6

Преобразуем узлы:

х₀′=x_3;

x₁′=x₄;

x₂′=x₂;

x₃′=x₅ ;

 Разделенные разности

 

Пусть функция ¦(c),задана на системе неравно отстоящих узлов.

Разделенной разностью 1-го порядка назовем выражение:

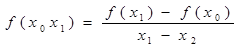
Разделенной разностью 2-го порядка:

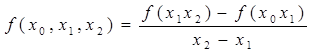
Разделенной разностью k-го порядка:

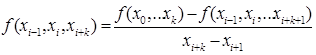                      (8.6)

|x-x₀|,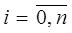

 

Свойства разделенной разности:

- на сетке равноотстоящих узлов разделенной разности совпадают конечными разностями

- разделенные разности понижают степень многочлена

- разделенные разности n-го порядка постоянны и равны