Уравнение 2-го порядка

D < 0 D = 0 D > 0

x Î Æ x 1 x 1; x 2

не имеет корней имеет один корень имеет два корня

Квадратное уравнение:            ax² + bx + c = 0

Если

то уравнение

Дискриминант:    D = b² – 4ac   

 

Формула корней:

Разложение на линейные множители: ax² + bx + c = a (x – x ₁) (x – x ₂)

Приведенное квадратное уравнение: x 2 + px + q = 0

Теорема Виета:

x 1 + x 2 = - p x 1 × x 2 = q

Примечание: m² + n ² = (m + n)² – 2 mn; m ³ + n ³ = (m + n)³ – 3 mn (m + n).

Следовательно,    x ₁² + x ₂² = p ² – 2 q;           x ₁³ + x ₂³ = p ³ + 3 pq

Эквивалентное уравнение: ax² + bx + c = 0 Û y² + by + c × a = 0 Þ x ₁ = y₁ /a; x ₂ = y ₂ /a

Однородное уравнение 2-го порядка относительно выражений  и :

. При решении однородного уравнения рассматривают два случая:

• Если = 0, то и = 0, то есть получим систему
• Если 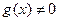, то, разделив все члены уравнения   на , сократив получившиеся дроби и, заменив одинаковые выражения новой переменной, составим систему, содержащую квадратное уравнение с новой переменной:

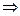
Уравнение n-го порядка    = 0

Имеется два основных метода решения: метод разложения на множители и метод введения новой переменной. При решении уравнений высших степеней используются теоремы:

• Если все коэффициенты многочлена P (x) = - целые числа и если x = a - целочисленный корень многочлена P (x), то число a является делителем свободного члена многочлена P (x).
• Если x = a - корень многочлена P (x), то P (x) делится без остатка на двучлен x - a.
• Если приведенное уравнение с целыми коэффициентами имеет рациональный корень, то этот корень обязательно является целым числом.
• Если коэффициент при старшей степени многочлена P (x) равен 1, целый корень многочлена P (x) является делителем свободного члена многочлена P (x) - .
• Если многочлен P (x) имеет рациональный корень , является делителем свободного члена многочлена P (x) - , а  является делителем старшего коэффициента многочлена P (x) - .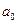

Решение дробно-рациональных уравнений вида , в общем случае сводится к решению целых уравнений вида  при условии .

Схема Горнера

Если , , , то при делении  на  частное  имеет вид , где , , . Остаток r находится по формуле  

				….

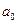
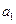
Корни многочлена

Корень многочлена  - число , такое, что

Число - k -кратный корень многочлена , если .

Если число  является k -кратным корнем многочлена , то при k> 1 оно будет (k - 1)-кратным корнем первой производной этого многочлена; при k = 1 число  не является корнем производной.

Формула Виета

Если = 0,  и - корни уравнения = 0, то корни можно подобрать по формуле Виета .