2020-05-12
253
Для задания движения естественным способом необходимо знать (рисунок 1.6):
1) траекторию точки (AB), т.е. уравнение
траектории
x = f ( y, z);
Рисунок 1.6
2) начало отсчета (точка O) с указанием направления движения («+» и « »);
3) закон движения
s = f (t)
– дуговая координата в функции времени,
которая должна быть однозначна, непрерывна и дважды дифференцируема.
Следует различать путь и дуговую координату.
Дуговая координата определяет положение точки на траектории относительно начала отсчета (точки O, см. рисунок 1.6).
Путь – расстояние пройденное точкой за некоторый промежуток времени вдоль траектории.
Допустим, за время t 1 точка переместилась из начального положения M 0
в положение
M 1 (рисунок 1.5), а за время t 2
из M 1 в точку O (таблица 1.1).
Таблица 1.1 – Отличие дуговой координаты от пути
| Время | Перемещение | Путь | Дуговая координата |
| t 0 | 0 | 0 | s = s 0 = OM 0 |
| t 1 | M 0 ® M 1 | M 0 M 1 | s = s 1 = OM 1 |
| t 2 | M 1 ® O | M 1 O | s = 0 |
| t 1 + t 2 | M 0 ® M 1 ® O | M 0 M 1 + M 1 O | s = 0 |
При естественном способе задания движения вводится система взаимно перпендикулярных осей (t, n, b), движущихся вместе с точкой и меняющих свое положение в пространстве – естественная система координат (рисунок 1.7).
|
|
|
Совокупность взаимно перпендику- лярных плоскостей, определяемых осями этой системы, называют подвижным трехгранником.
t, n, b – единичные векторы (орты) соответствующих осей:
Рисунок 1.7
b = t
´ n.
Орт t направлен по касательной к траектории в сторону увеличения дуговой координаты.
Орт n направлен перпендикулярно касательной оси t во внутрь вогнутой части траектории.
Орт b перпендикулярен t и n, и направлен в ту сторону, откуда виден кратчайший переход от t к n против хода часовой стрелки.
При движении точки, траектория всегда находится в соприка- сающейся плоскости, образованной осями t и n.
Скорость точки
u = dr
× ds = ds × dr
. (1.9)
dt ds dt ds
Вектор D r
D s
направлен также, как
вектор D r
(рисунок 1.8). При
D s ® 0
Рисунок 1.8
его направление стремится к направ- лению касательной, проведенной из точки M в сторону увеличения дуговой координаты s. Модуль этого вектора стремится к единице:
dr = lim D r = lim MM 1 = 1.
ds D s ®0 D s M 1® M MM 1
Таким образом, вектор dr
ds
имеет модуль, равный единице, и
направлен по касательной к траектории в сторону увеличения дуговой
координаты. Вектор dr
ds
является ортом t этого направления:
dr = t.
ds
Тогда уравнение (1.9) примет вид:
|
|
|
u = ds t.
dt
Производная ds
dt
есть проекция вектора скорости на касательную ось
t, т.е. определяет алгебраическую величину скорости:
u = ds. (1.10)
dt
Ускорение точки
a = du
= d
æ ds t ö = d (ut ) = du t
+ u dt .
dt dt ç dt ÷ dt dt dt
è ø
Производная du есть проекция вектора ускорения на касательную
dt
ось t:
– касательное (тангенциальное) ускорение, м/с2.
u dt
= u dt ds = u ds dt
= u 2 dt ;
dt = K =
1 n,
dt dt ds dt ds ds ds r
|
где K – вектор кривизны траектории;
r – мгновенный радиус кривизны траектории, м.
u dt
u 2
|
dt r
u 2
Отношение r есть проекция вектора ускорения на нормальную ось n:
2
– нормальное (центростремительное) ускорение, м/с.
Проекция вектора ускорения a на бинормальную ось b равна нулю, так как вектор ускорения расположен в соприкасающейся плоскости.
Тогда вектор полного ускорения будет равен:
du u 2
a = at + an = dt t +
r n.
По модулю ускорение равно:
a = =
. (1.11)
На рисунке 1.9 показаны векторы касательного at , нормального an и полного a ускорений движущейся точки M.
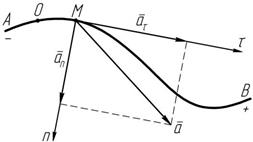
Рисунок 1.9
Касательное ускорение существует только при неравномерном движении точки и характеризует изменение скорости по величине.
Нормальное ускорение существует только при криволинейном движении точки и характеризует изменение скорости по направлению.
Касательное ускорение равно нулю, когда:
1) скорость постоянна по модулю;
2) скорость достигает экстремальных значений.
Нормальное ускорение равно нулю, когда:
1) скорость равна нулю;
2) траектория движения точки – прямая;
3) движущаяся точка совпадает с точкой перегиба траектории.
