2020-05-11
2898
Перед выполнением данного расчета необходимо вычертить упрощенно расчетную схему отдельно для быстроходного и тихоходного валов на миллиметровой бумаге формата А4.
При составлении расчётной схемы валы рассматривают как прямые брусья, лежащие на двух шарнирных опорах. Подшипники качения, воспринимающие радиальные и осевые силы, рассматривают как шарнирно–неподвижные опоры, а подшипники, воспринимающие только радиальные силы, как шарнирно–подвижные.
Внешние силы 
, 
, 
,действующие в полюсе зацепления, приводят к оси вала и изображают раздельно в вертикальной и горизонтальной плоскостях, при этом возникает изгибающий момент пар сил – 
. Здесь d 2 – делительный диаметр колеса.
По эскизной компоновке уточняют расстояния между точками приложения внешних сил к валу. Систему сил, действующих на вал, доводят до равновесного состояния, достраивая реакции в опорах.
Расчеты ведут, в следующей последовательности:
1. Определить реакции RА и RВ в опорах из условия равновесия вала, составляя уравнения статики: 
.
Правильность определения реакций RА и RВ проверяют с помощью уравнения 
.
2. Определить внутренние изгибающие моменты в поперечных сечениях на каждом участке вала методом сечений, составляя уравнения равновесия:
.
Под расчётной схемой вала строят эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях от всех действующих нагрузок. По этим эпюрам определяют результирующий изгибающий момент в любом сечении вала.
3. Определить величину суммарного изгибающего момента в каждом сечении вала по формуле:
где Мx, и Мy – изгибающие моменты в горизонтальной и вертикальной плоскостях соответственно, Н∙мм.
| 57 |
где Rx, и Ry – реакции опоры в горизонтальной и вертикальной плоскостях соответственно, Н.
Пример 1. Для вала колеса цилиндрического вертикального редуктора определить реакции опор подшипников. Построить эпюры изгибающих моментов.
Исходные данные: 
– окружная сила; 
– осевая сила; 
– радиальная сила; 
– сила от действия муфты;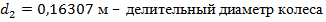 
; 
– длина пролета; 
– длина консоли.
1. Вычертим расчетную схему вала (рис. 20). Нанесем необходимые размеры, силы в зацеплении и консольную силу.
Действие осевой силы 
заменим изгибающим моментом 
, величину которого определим по формуле:
2. Расслоим расчетную схему на горизонтальную и вертикальную плоскости. В вертикальной плоскости будут действовать усилия: , 
, 
, 
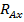в горизонтальной – 
, 
, 
, 
.
3. Определим реакции опор в вертикальной плоскости:
Проверка: 
;
4. Построим эпюру изгибающих моментов 
в вертикальной плоскости:
а) участок I: 
при 
при 
б) участок II: 
при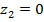 
при 
5. Определим реакции опор в горизонтальной плоскости:
| 58 |
Рис. 20. Расчетная схема вала колеса цилиндрического вертикального редуктора
| 59 |
Проверка: 
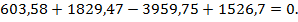
6. Построим эпюру изгибающих моментов Мy в горизонтальной плоскости:
а) участок I
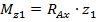
при
при 
б) участок II: 
при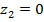
при 
в) участок III: 
при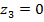 
при 
7. Определим суммарные реакции опор:
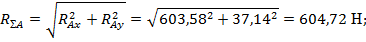
8. Вычислим суммарные изгибающие моменты и построим эпюру суммарных моментов:
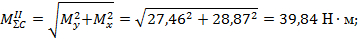
Пример 2. Для вала–шестерни конической определить реакции опор подшипников. Построить эпюры изгибающих моментов.
Исходные данные: 
– окружная сила; 
– осевая сила; 
– радиальная сила; 
–сила от действия открытой передачи;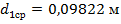 
– средний делительный диаметр шестерни; 
– длина пролета; 
– длина пролета между подшипниками; 
– длина консоли.
1. Вычертим расчетную схему вала (рис. 21). Нанесем необходимые размеры, силы в зацеплении и консольную силу.
Действие осевой силы 
заменим крутящим моментом 
, величину которого определим по формуле:
2. Расслоим расчетную схему на горизонтальную и вертикальную плоскости. В горизонтальной плоскости будут действовать усилия: , 
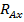, , в вертикальной – 
, 
, , .
3. Определим реакции опор в горизонтальной плоскости:
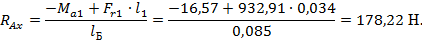
| 60 |
| 61 |
Проверка: 
4. Построим эпюру изгибающих моментов 
в горизонтальной плоскости:
а) участок I: 
при 
при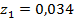 
б) участок II: 
при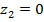
при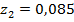 
5. Определим реакции опор в вертикальной плоскости:
Проверка: 
6. Построим эпюру изгибающих моментов Мx в вертикальной плоскости:
а) участок I
при
при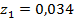 
б) участок II:
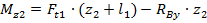
при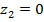 
при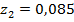 
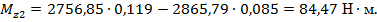
в) участок III: 
при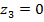 
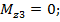
при 
7. Определим суммарные реакции опор:
8. Вычислим суммарные изгибающие моменты и построим эпюру суммарных моментов:
Пример 3. Для вала–червяка определить реакции опор подшипников. Построить эпюры изгибающих моментов.
| 62 |
Исходные данные: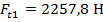 
– окружная сила; 
– осевая сила; 
– радиальная сила; 
– сила от действия муфты; 
; 
; 
– делительный диаметр червяка.
1. Вычертим расчетную схему вала (рис. 22). Нанесем необходимые размеры, силы в зацеплении и консольную силу.
Действие осевой силы заменим крутящим моментом , величину которого определим по формуле:
2. Расслоим расчетную схему на горизонтальную и вертикальную плоскости. В вертикальной плоскости будут действовать усилия: , , , 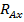в горизонтальной – , , , .
3. Определим реакции опор в вертикальной плоскости:
Проверка: 
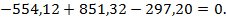
4. Построим эпюру изгибающих моментов в вертикальной плоскости:
а) участок I: 
при
при 
б) участок II: 
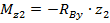
при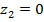
при 
5. Определим реакции опор в горизонтальной плоскости:
Проверка: 
6. Построим эпюру изгибающих моментов Мy в горизонтальной плоскости:
а) участок I 
| 63 |
Рис. 22. Расчетная схема вала червяка
| 64 |
при
при 
б) участок II: 
при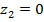 
при 
в) участок III: 
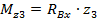
при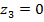
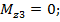
при 
7. Определим суммарные реакции опор:
8. Вычислим суммарные изгибающие моменты и построим эпюру суммарных моментов:
| 65 |
