2020-05-25
124
Достаточные условия оптимальности управления с полной обратной связью определяются следующей теоремой.
Теорема. Если существует функция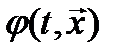 
, удовлетворяющая уравнению Беллмана
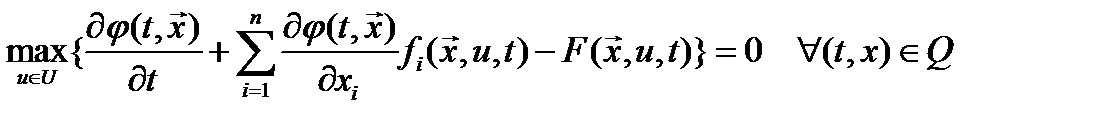(5)
с граничными условиями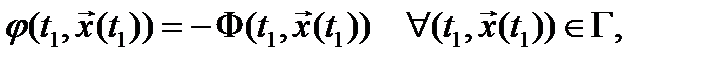 
и управление 
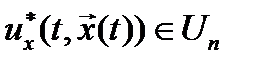, удовлетворяющее условию
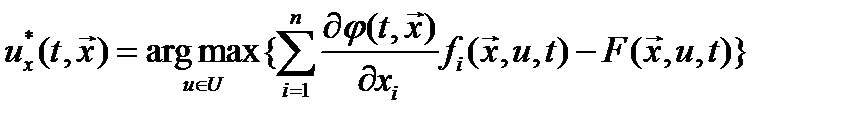, (6)
то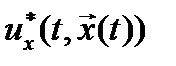 
является оптимальным управлением с полной обратной связью в задаче (4).
При этом минимальное значение функционала равно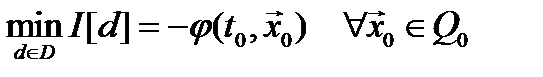 
.
Примечание. Аргумент максимизации (argmax или arg max) — значение аргумента, при котором данное выражение достигает максимума. 
argmax x f (x) {\displaystyle {\underset {x}{\operatorname {argmax} }}\,f(x)}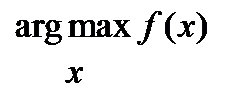 
есть значение х x {\displaystyle x}, при котором 
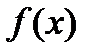f (x) {\displaystyle f(x)} достигает своего наибольшего значения. Является решением задачи 
argmax x f (x) ∈ { x | ∀ y: f (y) ≤ f (x) } {\displaystyle {\underset {x}{\operatorname {argmax} }}\,f(x)\quad \in \quad \{x\ |\ \forall y:f(y)\leq f(x)\}}
Аргумент максимизации определяется единственным образом тогда и только тогда, когда максимум достигается в единственной точке: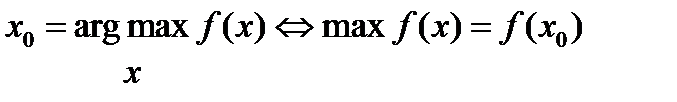 
x 0 = argmax x f (x) ⇔ max f (x) = f (x 0) {\displaystyle x_{0}={\underset {x}{\operatorname {argmax} }}\,f(x)\Leftrightarrow \max f(x)=f(x_{0})}
|
|
|
Если же максимум достигается в нескольких точках, то argmax может быть расширен до набора решений.
