2020-06-29
50
19.4.1. 
19.4.2. 
19.4.3 
19.4.4. 
19.4.5. 
19.4.6. 
19.4.7. 
Ответы. 19.4.1. 
и 
19.4.2. 
19.4.3. 
19.4.4. 
19.4.5. 
19.4.6. 
19.4.7. 
19.5. Однородные уравнения. Решения типовых задач
Однородные уравнения могут быть записаны в виде 
а также в виде 
где 
и 
— однородные функции одной и той же степени. (Функция называется однородной функцией степени 
, если для всех 
имеем 
) Чтобы решить однородное уравнение, можно сделать замену 
после чего получается уравнение с разделяющимися переменными.
19.5.1. Решить уравнение 
Решение. Это однородное уравнение. Пусть 
Тогда 
Подставляя в уравнение, получим 
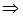
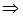
Возвращаясь к старому переменному 
запишем 
Кроме того, имеется решение 
которое было потеряно при делении на 
Ответ: 
.
19.5.2. Решить уравнение 
Решение. 
Подставляем в уравнение 
; сокращая на 
, получим:
Разделяя переменные и затем интегрируя, имеем:
Переходя к старым переменным, получим окончательный ответ: 
.
19.5.3. Решить уравнение 
Решение. 
Проведём замену 
и подставим ее в уравнение: 
. Разделяя переменные 
и интегрируя, запишем
. Возвращаясь к старым переменным, получим ответ: 
Уравнение вида 
приводится к однородному с помощью переноса начала координат в точку 
пересечения прямых 
и 
заменой 
. Если же эти прямые не пересекаются, то 
следовательно, уравнение имеет вид 
и приводится к уравнению с разделяющимися переменными заменой 
см. замечание в п. 19.2 и пример 19.3.3.
19.5.4. Решить уравнение 
Решение. 
. Это уравнение, приводящееся к однородному с помощью параллельного переноса осей координат: 
Решая систему линейных уравнений 
, найдём: 
.
Отсюда 
— однородное уравнение. Проводим известные уже замены 
Возвращаясь к старым переменным, получим окончательный ответ 
19.5.5. Решить уравнение 
Решение. 
подставим в уравнение: 
. Разделяя переменные 
и интегрируя, после возвращения к старым переменным, получим ответ 
Задачи для самостоятельного решения
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
19.6.1. 
19.6.2. 
19.6.3. 
19.6.4. 
19.6.5. 
19.6.6. 
Ответы. 19.6.1. 
19.6.2. 
19.6.3. 
19.6.4. 
19.6.5. 
19.6.6. 
