Первые интегралы нормальных систем ДУ

Опр.  Равенство

 

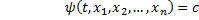
называется первым интегралом системы 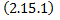в области 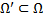, если выполняется 2 условия:

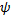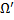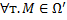
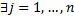1. Функция  имеет непрерывные частные производные 1-го порядка в области  и для , что .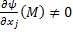

2. Для 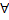 решения системы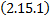

.                                

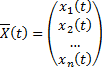
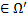
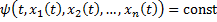Первый интеграл позволяет понизить число уравнений в системе. Пусть в т. 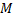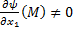. Тогда по теореме о неявной функции из  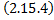можно в некоторой окрестности т.  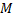выразить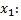

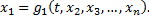
Подставив 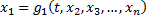 в уравнения системы 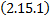, начиная со второго, получим систему из (n-1) уравнения:

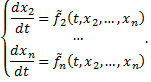
Чтобы полностью решить систему 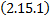, нужно знать  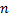независимых первых интегралов:

Независимость первых интегралов означает, что ни один из них не может быть выражен через остальные. Система 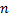 независимых первых интегралов  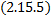неявно задает решение системы.

Симметричная форма записи нормальных систем ДУ:

Получив из симметричной формы системы интегрируемые комбинации (полные дифференциалы), можно найти 1-е интегралы. При нахождении интегрируемых комбинаций удобно использовать следующее свойство пропорций:

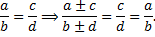
Пример 1.

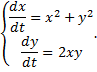
Симмметричная форма системы:

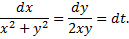
По свойству пропорций получаем

                                                                            

 

 

 

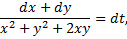
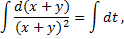
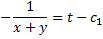
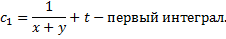
Аналогично

 

 

 

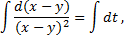
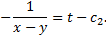
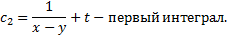
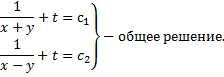
Пример 2.

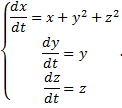
Для автономной системы найдем два независимых 1-х интеграла, не содержащих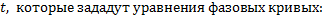

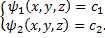
Симметричная форма системы:

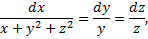
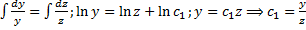 - (1-й интеграл).

Чтобы найти второй 1-й интеграл запишем симметричную форму системы в виде

 

,

 

 

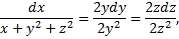
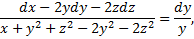
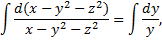
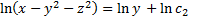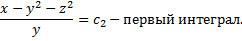
Таким образом, найденные первые интегралы задают фазовые кривые системы:

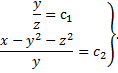
Пример 3.

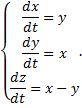
Симметричная форма:

,

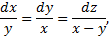
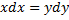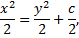
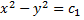-  1-й интеграл.

 

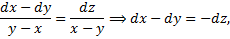
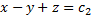 - 1-й интеграл.

 

 

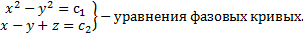
2.16.Нормальные системы ЛДУ, однородные и неоднородные. Матричная запись системы. Линейность пространства решений системы ЛОДУ. Вронскиан системы вектор-функций и его свойства. Теорема о размерности пространства решений системы ЛОДУ. Структура общего решения. Фундаментальная система решений.

 

 

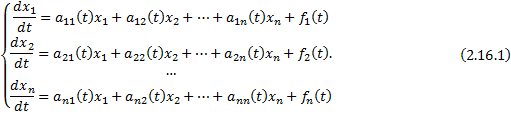
– нормальная система ЛНДУ, здесь 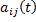,  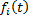– функции, непрерывные на некотором интервале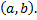

Если 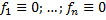, то 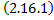 – система ЛОДУ.

Матричная форма системы ЛДУ :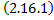

где

матрица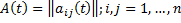

.

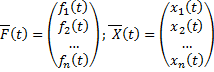Соответствующая

Теорема. Множество всех частных решений системы ЛОДУ 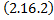 является линейным пространством относительно операций сложения вектор-функций и их умножения на число.

Док-во: пусть 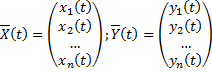 – решения системы 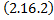. Рассмотрим вектор-функцию 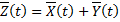. Имеем

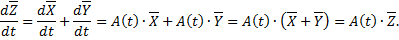
т.е. 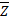 – решение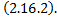

Аналогично при 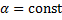 и вектор-функции  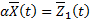получаем

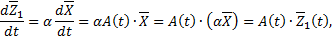
т.е. 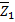 удовлетворяет системе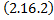 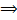 решения  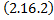образуют линейное пространство.

 

Опр.  Вронскианом системы вектор-функций

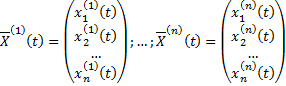
называется определитель 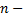го порядка

.

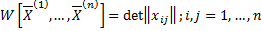Теорема (о вронскиане системы линейно зависимых вектор-функций).

Пусть вектор-функции 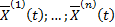 линейно зависимы на 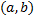. Тогда для .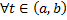

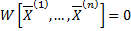Теорема (о вронскиане системы линейно независимых частных решений ЛОДУ)

Пусть 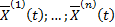 – линейно независимые частные решения системы ЛОДУ 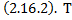огда для .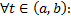

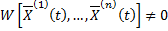Теорема (о структуре общего решения нормальной системы ЛОДУ).

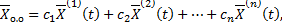
где 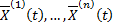 – линейно независимые частные решения системы 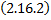;  – произвольные постоянные.

Док-во:

1. Покажем, что 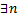 линейно независимых частных решений. Пусть  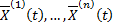– решения задачи Коши для системы 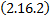с начальными условиями:

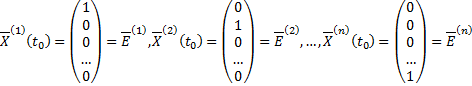
для некоторой .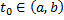

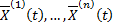 линейно независимы, т.к.

2. Покажем, что произвольное решение задачи Коши для (2.16.2) с начальным условием 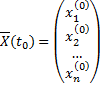  является линейной комбинацией .

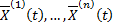Покажем, что заданному начальному условию удовлетворяет вектор-функция

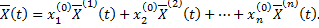
Действительно,

.

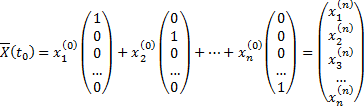Т.е. линейная комбинация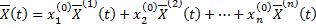

 удовлетворяет заданному начальному условию.

Таким образом любое решение является линейной комбинацией .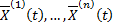

Опр. Система 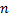 линейно независимых решений системы 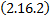называется фундаментальной системой решений (ФСР).

Теорема (о структуре общего решения системы ЛНДУ).

.

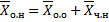Системы ЛОДУ с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения по корням характеристического уравнения (вывод для случая вещественных различных корней).

 

Система ЛОДУ с постоянными коэффициентами:

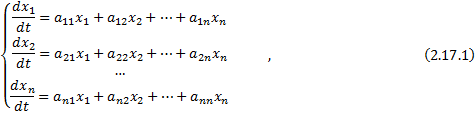
где ; .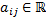

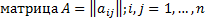Матричная форма:

Найдем решение вида 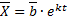, где .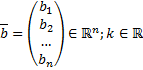

Подставим в :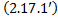

,

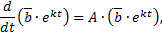
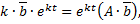
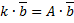 т.е. 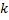 - собственное значение матрицы 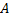;  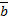– соответствующий собственный вектор.

Опр. Характеристическим уравнением системы ЛОДУ с постоянными коэффициентами 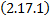называется характеристическое уравнени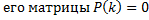е , где .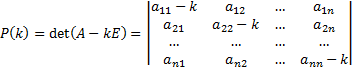

Построение ФСР для системы 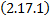по корням характеристического уравнения.

1. Случай различных действительных корней.

Пусть 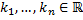 - различные корни характеристического уравнения (т.е. собственные значения матрицы ),

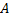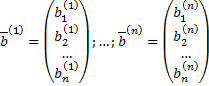  – соответствующие собственные вектора.

Тогда вектор-функции 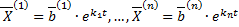 образуют ФСР для системы .

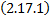Док-во: нужно доказать, что частные решения 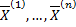линейно независимы.

Вронскиан 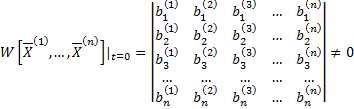, т.к. собственные вектора 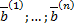линейно независимы (как собственные вектора, соответствующие различным собственным значениям), т.е. столбцы матрицы линейно независимы.

.

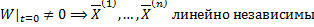Пример.

.

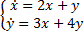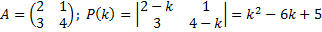
(можно использовать, что для матрицы 2Х2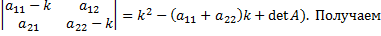

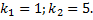
Найдем собственные значения.

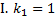; собственный вектор  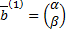находим из СЛАУ

,

,

.

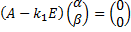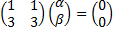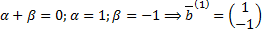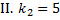; собственный вектор  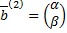находим из СЛАУ

,

.

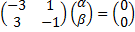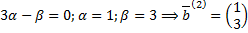ФСР: ,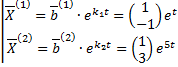

,

.

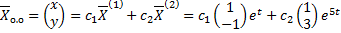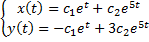2. Случай кратных действительных корней.

Пусть 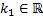 - корень характеристического уравнения кратности 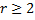. Ему соответствует решение вида

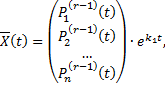
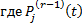 – многочлен степени 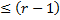. Коэффициенты находятся методом неопределенных коэффициентов.

Пример.

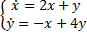
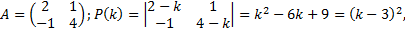
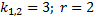
Ищем решение в виде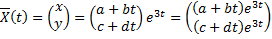

Подставим в систему:

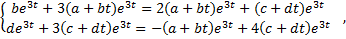
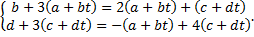
Коэффициент при 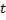 в 1-м уравнении: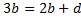

Коэффициент при 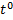 в 1-м уравнении: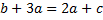

Коэффициент при 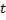 во 2-м уравнении: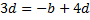

Коэффициент при 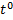 во 2-м уравнении: 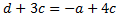. Получаем СЛАУ

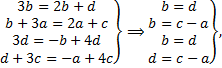
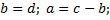
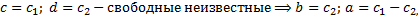
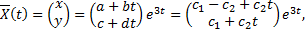
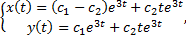
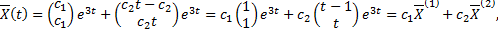
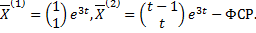
3. Случай комплексных корней кратности 1.

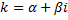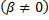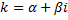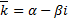Пусть  – корень кратности 1 . Паре корней  и  соответствуют 2 линейно независимых решения. Пусть  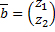– комплексный собственный вектор, соответствующий комплексному собственному значению 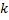. Он находится из СЛАУ .

.

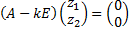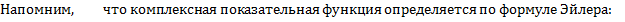
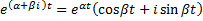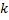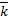Тогда корням  и  соответствует комплексное решение системы ДУ:

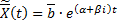
Тогда 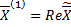 и 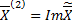 – вещественные линейно независимые решения, соответствующие корням  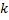и .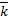

Пример.

,

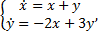
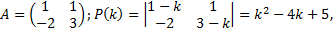
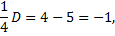
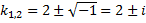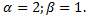
Найдем собственный вектор 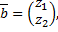  соответствующий :

,

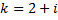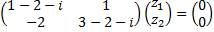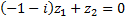 (второе уравнение пропорционально первому с коэффициентом ),

,

 

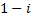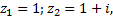
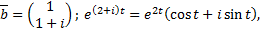
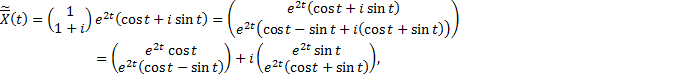
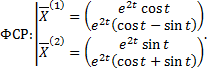
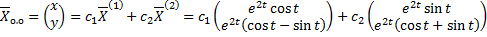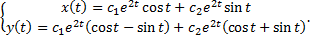
Литература

1. Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1988.-506 с. (Сер. Математика в техническом университете. Вып. VI).

2. Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1997.- 336 с. (Сер. Математика в техническом университете. Вып. VIII).

3.  Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. -М., Наука, 1981.

4.  Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. - М.: Наука, 1981.

5. Филиппов А.Ф. Введение в теорию дифференциальных уравнений. М.:УРСС, 2004.