Проекция вектора на ось

Понятие базиса.

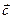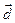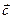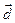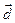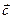Определение. Три линейно независимых вектора ,  и  образуют в пространстве базис, если любой вектор  может быть представлен в виде некоторой линейной комбинации векторов ,  и , т.е. если для вектора  найдутся такие вещественные числа l, m, n, что справедливо равенство: =l +m +n                            (1)

Определение. Два лежащих в плоскости p линейно независимых вектора  и  образуют на этой плоскости базис, если любой лежащий в плоскости p вектор 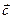 может быть представлен в виде некоторой линейной комбинации векторов  и , т.е. если для любого лежащего в плоскости p вектора 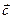 найдутся такие вещественные числа l и m, что справедливо равенство:  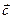    =l +m                         (2)

Утверждения.

1) любая тройка некомпланарных векторов ,  и 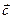 образует базис в пространстве;

2) любая пара лежащих в данной плоскости неколлинеарных векторов  и  образует базис на этой плоскости.

В дальнейшем для определенности будем рассматривать базис в пространстве.

Пусть ,  и 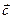 - произвольный базис в пространстве (т.е. произвольная тройка некомпланарных векторов). Тогда равенство 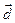=l +m +n 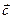 называется разложением вектора  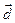по базису , , , 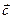а числа l, m, n - координаты вектора  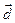относительно базиса , , .

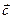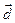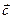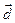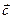Покажем единственность разложения вектора  по базису , , . Допустим противное, что наряду с разложением (1), справедливо еще и другое разложение по этому же базису: =l¢ +m¢ +n¢                    (3)

Вычитая из (1) из (3) получаем:

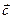(l-l¢) +(m-m¢) +(n-n¢) =0

В силу линейной независимости базисных векторов , ,  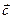последнее соотношение приводит к равенству: l-l¢=0, m-m¢=0, n-n¢=0 или l=l¢, m=m¢, n=n¢.

Теорема. При сложении двух векторов  и  их координаты (относительно любого базиса , , 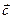) складываются. При умножении вектора  на любое число a все его координаты умножаются на это число.

Доказательство. Пусть =l₁ +m₁ +n₁ , =l₂ +m₂ +n₂ 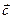. Тогда в силу свойств линейных операций:

+ =(l₁+l₂) +(m₁+m₂) +(n₁+n₂) ,

a =(al₁) +(am₁) +(an₁)

В силу единственности разложения по базису                                                ч.т.д.

Проекция вектора на ось.

(Ортогональная) проекция точки на ось – основание перпендикуляра, опущенного из точки на данную ось. (рисунок)

l

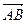Проекцией вектора  на ось u называется величина (длина) вектора 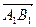, проведенного из проекции начала в проекцию конца вектора 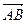, взятая со знаком “+”, если направление вектора  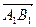совпадает с направлением оси u и со знаком “-” в противном случае.