Треугольник Паскаля и Бином Ньютона

Выше мы вычисляли число сочетаний C_n^m непосредственно по формуле, делая много умножений и делений. Оказывается, есть метод вычислять сразу много разных "цэшек", используя только сложение. Особенно важно это при программной реализации, поскольку компьютер складывает числа гораздо быстрее, чем умножает и тем более делит. Он основан на доказанном выше "свойстве 2": C_n+1^m+1=C_n^m + C_n^m+1.

Давайте построим из чисел два бесконечных треугольника. В первом из них (см. рис. внизу слева) будем ставить единицы в самом верху и по краям каждом следующей строки, а каждое из остальных чисел будет равно сумме двух стоящих над ним слева и справа (этот треугольник называется треугольником Паскаля – Блез Паскаль (1623-1662) – французский математик). Во втором (см. рис. внизу справа) будем последовательно выписывать значения C_n^m, отводя по одной строке для каждого значения n и располагая в ней "цэшки" по возрастанию m. На самом деле эти треугольники одинаковы. Равенство первых нескольких строчек, можно заметить, а дальше надо уже доказывать.

Утверждение. Если строчки треугольника Паскаля и позиции в них нумеровать, начиная с нуля, то на m-м месте в n-й строке будет стоять значение C_n^m (основное свойство треугольника Паскаля).

Доказательство: Индукция по n (см. лекцию "Индукция", если вы еще не знакомы с этим методом).

База: n=0 – действительно, C₀⁰=1 – как раз то, что стоит на верхушке треугольника Паскаля.

Переход: от n к n+1. Пусть в n-й строчке все числа уже равны значениям "цэшек" из n по соответствующим m. Рассмотрим n+1-ю строчку. На ее краях (нулевое и n+1-е места) стоят две единицы – и значения C_n+1⁰ и C_n+1ⁿ⁺¹ как раз равны 1. Далее, при всех m от 1 до n число, стоящее на m-м месте в n+1-й строке, равно сумме чисел, стоящих в n-й строке на m-1-м и m-м местах соответственно (т.е. как раз двух стоящих над ним – по принципу построения треугольника Паскаля). По предположению индукции, они равны C_n^m-1 и C_n^m, а их сумма тогда будет C_n^m-1+C_n^m, что как раз равно C_n+1^m (по свойству 2 "цэшек"), ч.т.д.

Для справки мы приводим здесь первые 11 строчек (с нулевой по 10-ю) треугольника Паскаля – их можно посчитать и вручную. На компьютере, с помощью простой программы, можно вычислить значительно больше "цэшек", и более быстрого алгоритма, чем треугольник Паскаля, пока не существует.

Такие, казалось бы, чисто комбинаторные вещи, как числа C_n^m и треугольник Паскаля, неожиданно встречаются и в алгебре. Выпишем известные формулы сокращенного умножения:

Коэффициенты в этих формулах (и это лучше видно, когда выписаны еще нулевая и первая степень) – это числа из треугольника Паскаля, то есть "цэшки". На самом деле, такая закономерность будет продолжаться и дальше, и называется она бином Ньютона.

Точнее:

(a+b)ⁿ = aⁿ+C_n¹a^n-1b+C_n²a^n-2b²+...+C_n^n-1a¹b^n-1+bⁿ =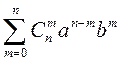

Можно доказать эту формулу по индукции, как и основное свойство треугольника Паскаля. Но приведем более простое объяснение:
(a+b)ⁿ=(a+b)(a+b)...(a+b) – n скобок. Раскрывая скобки, получаем в отдельных слагаемых произведения n букв, каждая из которых – a или b, т.е. a^n-mb^m при каком-то m от 0 до n. Докажем, что для каждого такого m число таких слагаемых – ровно C_n^m, откуда, приведя подобные, и получаем формулу бинома. Но это правда: a^n-m b^m получается путем взятия a из m скобок и b из n-m оставшихся; разные такие слагаемые получаются путем разного выбора этих самых m скобок, а m скобок из n можно выбрать как раз C_n^m способами, ч.т.д. (!)

Именно из-за бинома Ньютона числа C_n^m часто называют биномиальными коэффициентами.