Выбор рациональной схемы маршрута

Пусть известна транспортная сеть города, состоящая из узлов (центров, микрорайонов) и ребер (улиц), по которым организовано движение автомобильного транспорта, которые соединяют между собой узлы.

Каждому узлу транспортной сети соответствует величина t_рi численно равная затратам времени на посадку в пункте i. Каждому ребру соответствует величина t_слij численно равная затратам времени на следование между пунктами i и j. Известно расстояние между пунктами i и j, т.е. длина ребра l_ij.

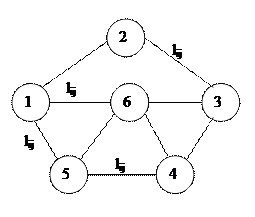
Задана матрица пассажирских корреспонденций между всеми микрорайонами города за определенный период суток. Причем элемент Р_ij (подвижность населения) соответствует числу передвижений, совершаемых из пункта i в пункт j. Зная это, можно составить большое количество комбинаций маршрутов, соединяющих между собой узлы транспортной сети. Каждой комбинации соответствует число Е, численно равное суммарным затратам времени всех пассажиров на передвижение по все маршрутам, включая затраты времени на следование, ожидание и пересадки.

Схема маршрутов с минимальными суммарными затратами времени на передвижение является рациональной.

При решении дальнейшей оптимизации маршрутов принимается, что пешие подходы от и до остановочного пункта зависят не от схемы маршрута, а от разветвленности транспортной сети.

Если принять, t_{подх/отх}=const, то в процессе решения задачи требуется минимизировать

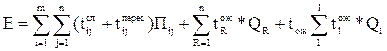
где i – пункт начала передвижения;

j – пункт окончания передвижения;

m,n – количество узлов;

R – количество маршрутов автобусов;

l – совмещенные участки транспортной сети;

t_слij, t_ожij, t_пересij – затраты времени на следование, ожидание и пересадку 1-го пассажира;

П_ij – число передвижений между i и j;

t_ожR – затраты времени 1-го пассажира на ожидание начала поездки на маршруте R;

Q_R – количество пассажиров, пользующихся только маршрутом R;

t_ожl - затраты времени 1-го пассажира на ожидание начала поездки для 2-х и более маршрутов;

Q_l – число пассажиров, проезжающих по совмещенному участку l.

В целях сокращения количества сравниваемых вариантов маршрутных схем, а также для учета реальных условий перевозок, в каждом конкретном городе при выборе рациональной схемы учитывается дополнительное условие ограничения.

В большинстве городов перевозка пассажиров осуществляется по ложившейся схеме маршрута, который в большинстве случаев является не оптимальной. В этих городах действуют маршруты, установленные на основе многолетней практической работы, поэтому возможны случаи когда некоторые хорошо зарекомендовавшие себя маршруты изменять нецелесообразно. Такие маршруты следует включить в рациональную схему без изменения, они считаются заданными. Кроме того, есть маршруты неподлежащие включению в рациональную схему, такие маршруты называются запрещенные.

Исходные данные, используемые при расчете схем маршрутов и подготавливаемые АТП разбивают на 3 группы:

1. маршруты, которые имеют постоянные маршруты (общее количество микрорайонов в городе, продолжительность расчетного периода времени, максимальное возможное количество остановок на 1-м маршруте, средняя вместимость 1-го автобуса, коэффициент внутричасовой неравномерности пассажиропотока и коэффициент неравномерности подхода пассажира к остановочному пункту).

Кроме того, в эту группу включены ограничения:

- максимально-допустимая длина маршрута

- максимальный интервал

- максимальное количество автобусов на маршруте

- минимальный допустимый средний уровень наполнения

- общее число микрорайонов закрытых для организации конечных пунктов

- количество маршрутов обязательно включаемых в рациональный вариант схемы маршрутов

2. маршруты, размеры которых непостоянны и зависят от общего числа микрорайонов, числа запрещенных маршрутов, количества заданных маршрутов (номера микрорайона охваченными маршрутами, затраты времени на посадку в каждом микрорайоне и пересадки, номера микрорайонов для организации конечных остановок, номера конечных и промежуточных пунктов на каждом заданном маршруте)

3. маршруты, исходные размеры которых непостоянны и зависят от количества микрорайонов (количество перемещений населения между каждой парой микрорайонов, характеристика участков транспортной сети, в т.ч. длина маршрута и время следования).

Решение задачи по выбору рациональной схемы начинается с установления возможных маршрутов, т.е. тех из которых можно формировать различные варианты маршрутных схем. В целях сокращения этих вариантов принято соблюдение следующих условий:

Маршрут между 2-мя пунктами может быть открыт только по пути с минимальными затратами времени на следование автобусов между ними. Приняв такое условие общее количество возможных маршрутов можно посчитать

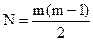, m – число микрорайонов

Задача нахождения кратчайших путей относится к комбинаторных. Для ее решения территория графа.

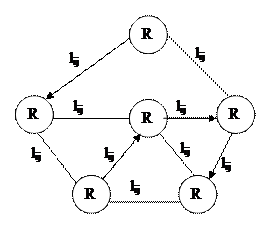Графом называется совокупность ее узлов R и соединяющих ее дуг протяженностью l_ij. За вершины графа принимаются центры транспортных районов и обозначаются буквой R, а дугами изображают улицы транспортной сети, а также пути пешеходного потока к остановочным пунктам пассажирского транспорта.

Дуги, допускающие движение только в одном направлении называются ориентированными, а графы называются ориентированными. Дуги, допускающие движение только в обоих направлениях называются неориентированными.

В общем случае транспортная сеть – это совокупность ориентированных и неориентированных дуг и такой граф называется смешанным.

Тема 2. Выбор подвижного состава.