Критическое давление и скорость. Сопло Лаваля

Первый закон термодинамики для потока

Термодинамика потока

На практике при рассмотрении рабочих процессов машин, аппаратов и устройств, встречаются задачи изучении закономерностей движения рабочих тел (газов, пара и жидкостей).

Уравнение 1-го закона термодинамики для потока газа при следующих допущениях:

- движение газа по каналу установившееся и неразрывное;

- скорости по сечению, перпендикулярному оси канала, постоянны;

- пренебрегается трение частичек газа друг другу и о стенки канала;

- изменение параметров по сечению канала мало по сравнению их абсолютными значениями и согласно закону сохранения энергии имеет вид:

q=Du+De+l_прот.+l_техн., (1.45)

где De = (w²₂ – w²₁)/2 + g·(z₂ –z₁) – изменение энергии системы, состоящее из изменения кинетической и потенциальной энергий; w₁,w₂ – скорости потока в начале и в конце канала; z₁, z₂ – высота положения начала и конца канала; l_прот– работа проталкивания, затрачиваемая на движения потока; l_прот=P₂·v₂–P₁·v₁; l_техн. – техническая (полезная) работа (турбины, компрессора, насоса, вентилятора и т.д.).

После подстановки значений величин в баланс (1,45) получаем

q=(u₂–u₁)+(w²₂–w²₁)/2+g·(z₂–z₁)+P₂·n₂–P₁·n₁+l_техн. (1.46)

Введем понятия энтальпии, которую обозначим через величину:

h=u+Pv, (5.3)

h₂=u₂+P₂·n₂; h₁=u₁+P₁·n₁. (1.47)

Тогда уравнение 1-го закона термодинамики для потока газа будет иметь вид:

q=h₂–h₁+(w²₂–w²₁)/2+g·(z₂–z₁)+l_техн. (1.48)

Если перемещение газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом.

Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называют диффузором.

В каналах при небольшой разности давлений газа и внешней среды скорость течения рабочего тела достаточно большая. В большинстве случаев длина канала небольшая и процесс теплообмена между стенкой и газом незначителен, поэтому процесс истечения газа можно считать адиабатным.

Скорость истечения (на выходе канала) определяется из уравнения:

w=w₂=(h₁–h₂)^0,5. (1.49)

или

w=v₂{P₁·v₁[1–(P₂/P₁)^(k-1)/k]/(k-1)}^0,5. (1.50)

Массовый секундный расход газа, [кг/с]:

m=f·w/v₂, (1.48)

где: f – площадь сечения канала на выходе.

Так как процесс истечения адиабатный, то v₂=v₁(p₂/p₁)^1/k. После подстановки и преобразований, получим:

m=f·{2kP₁/v₁·[(P₂/P₁)^2/k–(P₂/P₁)^(k+1)/g] /(k-1)}^0,5. (1.51)

Массовый секундный расход идеального газа зависит от площади выходного канала, начального состояния газа и степени его расширения.

Критическим давлением называется такое давление на выходном сечении канала, при котором достигается максимальный расход газа и определяется следующим выражением:

P_К=P₂=b_К·P₁, (1.52)

где: P_К=(2/(k+1))^k/(k-1).

Для одноатомных газов: k=1,66 b_К=0,49; для двухатомных газов: k=1,4 и b_К=0,528; для трехатомных газов: k=1,3 и b_К=0,546.

Критической скоростью называется скорость газа в выходном сечении канала, при давлении равном или меньшем критического - P_К.

w_К=[2(g/(g+1))·P₁·v₁]^0,5. (1.53)

Критическая скорость зависит при истечении идеального газа только от начальных параметров, его природы и равна скорости звука газа (а) при критических параметрах.

w_К=а=[k·P_К·v_К]^0,5. (1.54)

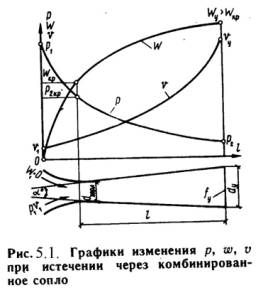Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для получения скоростей истечения, превышающих критическую или скорость звука. Сопло Лаваля состоит из короткого суживающегося участка и расширяющейся конической насадки (pис.1.8). Опыты показывают, что угол конусности расширяющейся части должен быть равен a=8¸12^о. При больших углах наблюдается отрыв струи от стенок канала.

Скорость истечения и секундный расход идеального газа определяются по формулам (1.50) и (1.51).

Длину расширяющейся части сопла можно определить по уравнению:

l=(D–d)/2·tg(j/2), (1.55)

где: j - угол конусности сопла; D - диаметр выходного отверстия; d - диаметр сопла в минимальном сечении.