Распределение концентрации неравновесных носителей заряда

Для нахождения закона изменения избыточной концентрации электронов вдоль оси x выделим внутри полупроводника элементарный объем, ограниченный сечениями x₁ и x₂, перпендикулярными оси x, приняв площадь сечений равной 1 см² (рис. 7.1). Тогда величина этого объема будет равна dx. В этот объем через сечение x₁ входит некоторое количество электронов n₁, часть электронов рекомбинирует с дырками, а некоторое количество электронов n₂ покидает этот объем через сечение x₂.

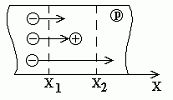
Рис.7.1

Количество электронов, диффундирующих через любое сечение х за время dt равно

. ,

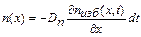где D_n — коэффициент диффузии электронов.

Знак «минус» указывает на то, что перемещение носителей заряда происходит в сторону убывания их концентрации.

Зная количество электронов, диффундирующих через сечения x₁ и x₂, и учитывая, что в объеме dx происходит рекомбинация со скоростью, определяемой уравнением (6.4), можно найти изменение концентрации электронов в объеме dx за время dt:

.

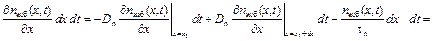
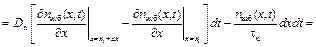
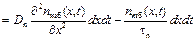Последнее уравнение можно записать в виде:

.

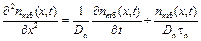Избыточные электроны за время жизни t_n диффундируют на расстояние 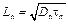, поэтому:

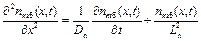. (7.1)

Полученное уравнение называется уравнением непрерывности для электронов. Оно характеризует изменение избыточной концентрации электронов, обусловленное диффузией и рекомбинацией. Интегрируя это уравнение при известных начальных и граничных условиях можно найти n_изб(x,t)

В случае, когда уменьшение концентрации электронов в элементарном объеме, вызванное рекомбинацией, компенсируется инжекцией в него новых электронов, избыточная концентрация электронов сохраняется неизменной во времени. Тогда уравнение (7.1) должно быть записано в виде:

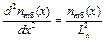. (7.2)

Решение этого уравнения имеет вид:

.

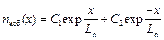Постоянные интегрирования С₁ и C₂ находят из следующих условий:

,

.

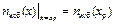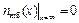Здесь n_изб(x_p) —концентрация электронов на поверхности полупроводника.

Следовательно, 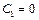и 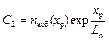. Тогда

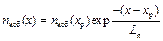. (7.3)

Таким образом, избыточная концентрация электронов изменяется вдоль оси x по экспоненциальному закону, а величина L_n, называемая диффузионной длиной, представляет собой расстояние, на котором избыточная концентрация уменьшается в е раз (рис. 7.2,а).

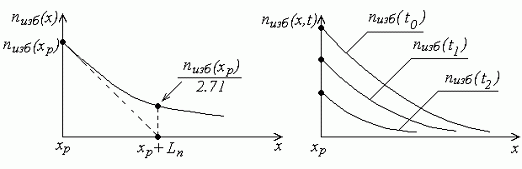
а) б)

Рис.7.2

После прекращения инжекции избыточная концентрация уменьшается с течением времени (рис.7.2,б)

8. Электронно–дырочный переход

Электронно–дырочным переходом, или p-n -переходом называют слой, возникающий на границе раздела двух полупроводников с различным типом электропроводности. Если п- и р-области разделены, то уровни Ферми разнесены на величину E_ПО=Е_Fn–E_Fp. Если п- и р-области каким-либо образом привести в состояние контакта (рис. 8.1,а), то возникнут диффузионные потоки электронов из п-области в р-область и дырок из р-области в п-область. При этом в п-области остаются положительные заряды ионизированных доноров, и она заряжается положительно, а в р-области остаются отрицательные заряды ионизированных акцепторов, и она заряжается отрицательно. В ходе диффузии все энергетические уровни в п-области понижаются, а в в р-области повышаются. Это происходит до тех пор, пока постепенно поднимающийся уровень Ферми в р-области не установится на одной высоте с постепенно опускающимся уровнем Ферми в п-области, в результате чего произойдет выравнивание уровней Ферми и энергетическая диаграмма примет вид, показанный на рис.8.1,б. При этом на границе раздела образуется энергетический барьер, высота которого равна разности уровней Ферми в неконтактируемом состоянии полупроводников:

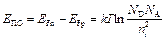. (8.1)

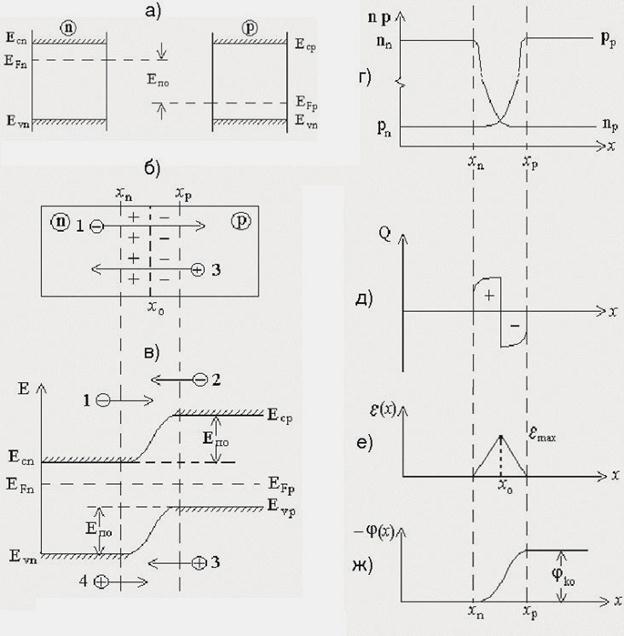
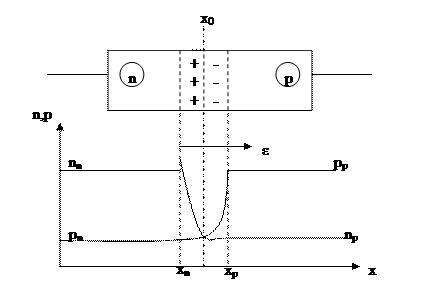
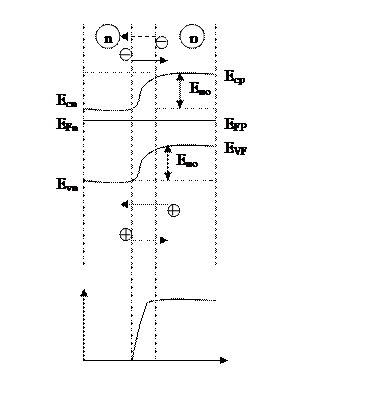
Рис.8.1

На рис.8.1 оставить рис.б,в,г и ж, расположив их друг под другом. Присвоить оставленным рисункам символы а,б,в и г.

Следствием диффузионного перемещения электронов и дырок является уменьшение их концентрации левее и правее границы раздела х_о (рис. 8.1,в), в результате чего между сечениями х_n и х_p образуется слой, обедненный подвижными носителями заряда. В этом слое концентрация доноров и акцепторов во много раз превышает концентрацию электронов и дырок, что позволяет пренебречь концентрацией подвижных носителей заряда. Заряды доноров и акцепторов создают внутреннее электрическое поле, которое препятствует диффузии и не позволяет выровняться концентрациям электронов и дырок по всему объему полупроводникового кристалла.

Распределение потенциала, характеризуемое потенциальной диаграммой φ(х), показано на рис.8.1,г, где за нулевой уровень принят потенциал п-области. Высота потенциального барьера j_ко связана с высотой энергетического барьера соотношением

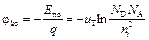. (8.2)

Ширина перехода равна ∆_о=(х_о-х_n)+(х_р-х_о). Заряд доноров в переходе равен Q_D=qN_D(x_o-x_n), откуда 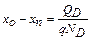. Заряд акцепторов равен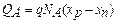, откуда 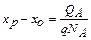. При N_D=N_A выполняется условие: x₀–x_n=x_p–x_0. Такой переход называют симметричным. Если N_D¹N_A, то такой переход называют несимметричным. В этом случае переход оказывается сдвинутым в область с более низкой концентрацией примесей.

Учтем, что Q_D=Q_A=Q. Следовательно

∆_о =.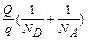

Заменим объемное распределение зарядов сосредоточенным на обкладках конденсатора, расположенных на расстоянии ∆_о/2. Заряд на обкладках такого конденсатора равен

Q=Cφ_ко.=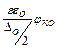

Следовательно,

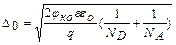. (8.3)

При N_D>>N_A уравнение (8.3) принимает вид:

.

При N_D<<N_A уравнение (8.3) принимает вид:

.

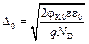Электроны (и дырки), находясь в хаотическом движении, способны перемещаться через электронно-дырочный переход из одной области полупроводникового кристалла в другую, создавая потоки носителей заряда, обозначенные на рис. 8.1 цифрами от 1 до 4. Потоки 1 и 3 называют потоками основных носителей заряда (ПОН), потоки 2 и 4 – потоками неосновных носителей заряда (ПНН). Для ПОН поле в переходе является тормозящим. Поэтому переходить из п -области в р -область могут только те электроны, энергия которых выше Е_cn и, соответственно, переходить из из р- области в п -область могут только те дырки, энергия которых ниже уровня Е _vp. Для ПНН поле в переходе является ускоряющим, поэтому все неосновные носители заряда способны перемещаться из одной области в другую. При отсутствии на переходе внешнего напряжения ПОН и ПНН уравновешивают друг друга, поэтому ток через переход равен нулю.

Если к переходу подключить внешнее напряжение u=φ_p-φ_n плюсом к р-области, а минусом к n-области, то создаваемое им электрическое поле будет противоположно по направлению с внутренним электрическим полем. В этом случае потенциальный барьер в p-n-- переходе уменьшится. При противоположной полярности внешнего напряжения потенциальный барьер повысится. Внешнее напряжение, уменьшающее высоту потенциального барьера в p-n-- переходе, называют прямым, а напряжение, повышающее высоту барьера, — обратным. В дальнейшем прямое напряжение будем считать положительным, а обратное — отрицательным. Внешнее напряжение практически полностью прикладывается непосредственно к p-n-- переходу, так как он обеднен подвижными носителями зарядов и имеет высокое по сравнению с другими областями структуры электрическое сопротивление. Поэтому изменение высоты потенциального барьера равно приложенному напряжению u, и высоту потенциального барьера в р-п -переходе следует определять по формуле:

.

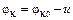Если к p-n- переходу приложено прямое напряжение, то вследствие уменьшения высоты потенциального барьера, возрастает количество основных носителей заряда, перемещающихся через p-n- переход. В результате появляется большой прямой ток, создаваемый потоками 1 и 3. Если к р-п-переходу приложено обратное напряжение, то количество основных носителей заряда, перемещающихся через переход, становятся равными нулю, и через переход течет небольшой обратный ток, создаваемый потоками неосновных носителей заряда (потоки 2 и 4). Таким образом, изменяя приложенное к p-n- переходу напряжение, можно изменять величину тока и его направление (рис.8.2)

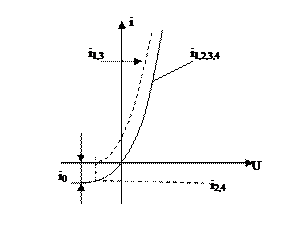
Рис.8.2

. При изменении приложенного к переходу внешнего напряжения одновременно с изменением высоты потенциального барьера изменяется ширина перехода. При подаче прямого напряжения переход сужается, а при подаче обратного напряжения расширяется.

9. Вольтамперная характеристика p-n -перехода

Для того чтобы выяснить, как зависит ток p-n- перехода от приложенного к нему напряжения, рассмотрим распределение концентрации неосновных носителей зарядов и токов в областях, прилегающих к p-n- переходу (рис. 9.1).

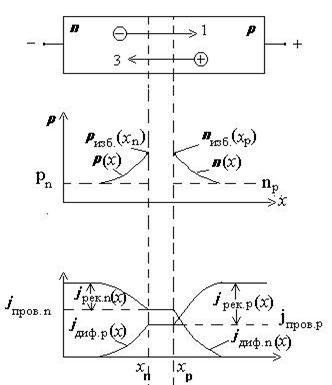
Рис.9.1

При подаче на p-n- переход прямого напряжения уменьшается высота потенциального барьера, возрастают потоки основных носителей заряда, и возникает инжекция электронов в p-область и дырок в n-область. Инжектированные электроны диффундируют вглубь p-области, и их концентрация по мере удаления отсечения x_p убывают по экспоненциальному закону. То же самое происходит с дырками, инжектированными в n-область. Неравномерное распределение концентрации неосновных носителей заряда ведет к возникновению токов диффузии j_диф.п(х) и j_диф.р(х),. Уход электронов из п-области (поток 1) в p-область ведет к возникновению тока проводимости электронов j_пров.п., который вдоль оси х сохраняется неизменным, так как на смену электронам, прошедшим через сечение х_р из внешней цепи поступают новые электроны. Аналогично в p-области возникает ток проводимости дырок j_пров.р. Внутри перехода электронный и дырочный токи не изменяются, так как считается, что в пределах сравнительно узкого перехода генерационно-рекомбинационными процессами можно пренебречь.

Из приведенных графиков распределения токов следует, что плотность тока через p-n- переход, равна сумме диффузионных токов на его границах:

j = j_диф.п(х_р)+j_диф.р(х_n).

Плотность тока диффузии электронов в сечении х_р пропорциональна градиенту концентрации электронов в сечении х_р, то есть, тангенсу угла наклона касательной к графику n(x) в сечении х_р:

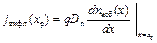. (9.1

Плотность тока диффузии дырок в сечении х_n пропорциональна градиенту концентрации дырок в сечении х_n, то есть тангенсу угла наклона касательной к графику р(х) в сечении х_n:

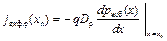. (9.2)

Градиент концентрации электронов в сечении х=х_р можно найти, дифференцируя (7.3):

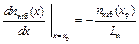. (9.3)

Соответственно градиент концентрации дырок в сечении х_n равен

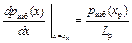. (9.4)

Избыточные концентрации электронов и дырок на границах p-n- перехода зависят от приложенного напряжения, изменяющего высоту потенциального барьера. При отсутствии внешнего напряжения высота барьера определяется (8.2). Учитывая, что N_D=n_n, N_A=p_p и 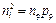, (8.2) можно представить в виде:

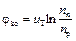. (9.5)

Отсюда получаем

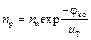. (9.6)

При подаче прямого напряжения потенциальный барьер становится равным j_К=j_ko–u, следовательно, концентрация электронов в сечении х_р становится равной

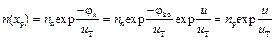(9.7).

Избыточная концентрация электронов равна

. (9.8)

Аналогично, избыточная концентрация дырок равна

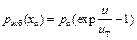. (9.9)

Подставляя (9.8) и (9.9) в (9.1) и (9.2), получим уравнения для электронного и дырочного токов на границах перехода:

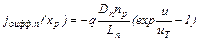, (9.10)

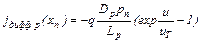. (9.11)

Суммируя диффузионные токи, получим уравнение вольтамперной характеристики:

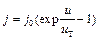, (9.12)

где

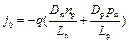. (9.13)

Ток j₀ называют тепловым током, поскольку он создается неосновными носителями заряда, возникающими в результате тепловой генерации. Знак минус указывает на то, что направление этого тока противоположно положительному направлению оси x.

При N_D>>N_A тепловой ток создается электронами, генерируемыми в р-области. В этом случае

.

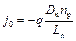При N_A>>N_D тепловой ток создается дырками, генерируемыми в п-области. Тогда

.

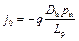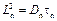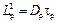Формулу (1.98) можно преобразовать, умножив числитель и знаменатель первой дроби на L_n, а второй — на L_p. Тогда, учитывая, что и , получим

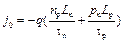. (9.14)

В этом выражении отношения n_p/t_n и p_n/t_p есть не что иное, как скорости генерации электронов и дырок соответственно. Следовательно, тепловой ток создается только теми неосновными носителями заряда, которые генерируются в объемах полупроводника, прилегающих к границам p-n- перехода. Величина этих объемов при площади p-n- перехода, равной единице, равна диффузионной длине неосновных носителей заряда. Носители заряда, генерируемые за пределами этих объемов, не могут участвовать в создании теплового тока, так как за время жизни они не в состоянии преодолеть расстояние, превышающее диффузионную длину, и достичь границы p-n- перехода. При N_D>>N_A в (9.14) можно пренебречь вторым слагаемым, а при N_A>>N_D - первым.

Вольтамперная характеристика для небольших прямых и обратных напряжений (|u|<3u_T),

представлена на рис. 9.2,а. При обратном напряжении, превышающем 3u_T, обратный ток не зависит от напряжения и равен j_о. При прямом напряжении u>3u_T отношение прямого тока к обратному составляет 10³…10⁴, поэтому приходится вводить разные масштабы для прямых и обратных токов и напряжений. При этом в области небольших прямых напряжений прямая ветвь характеристики сливается с горизонтальной осью, но это не означает отсутствие тока, просто этот ток столь мал, что масштабы графика не позволяют его отразить. Получается, что прямая ветвь характеристики оказывается смещенной вправо относительно нулевого напряжения (рис.9.2,б). Прямое напряжение, при котором прямой ток становится заметным, называют пороговым или напряжением отсечки.

В области прямых напряжений изменение напряжения на 60 мВ изменяет ток примерно в 10 раз. Поэтому в некоторых случаях целесообразно рассматривать зависимость напряжения от тока. Чтобы получить такую зависимость, надо решить (9.14) относительно напряжения. Тогда

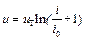. (9.15)

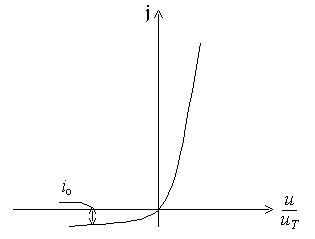
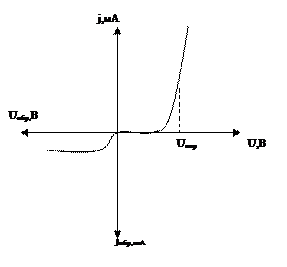
а) б)

Рис. 9.2

Обратный ток, создаваемый неосновными носителями заряда, сильно зависит от температуры, так как он пропорционален 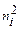. Зависимость обратного тока от температуры характеризуют температурой удвоения:

.

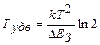При комнатной температуре она равна для кремния 5° С, для германия 8°С, для арсенида галлия 3,6°С.