Анализ и расчет простых электрических цепей переменного тока с помощью комплексных чисел

Анализ режимов в электрических цепях существенно упрос­тится и станет более наглядным, если воспользоваться комплексными числами, а векторные диаграммы напряже­ний и токов строить на комплексной плоскости. Уравнения электрического состояния для цепи переменного тока в ком­плексной форме сходны с уравнениями электрического сос­тояния для цепей постоянного тока. Благодаря этому анализ и расчет электрических цепей синусоидального тока с помощью комплексных чисел получил в практике широкое применение.

Сущность метода состоит в том, что в уравнениях электриче­ского состояния мгновенные значения тока и напряжения на всех участках заменяют комплексными. Так, мгновенные значения то­ка i и напряжения U заменяют комплексом тока 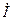и напряже­ния 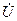. Мгновенное значение напряжения U_R =Ri на резистивном участке с сопротивлением R заменяют комплексом 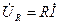, по фазе совпадающим с током 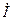. Мгновенное значение напряже­ния 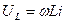на участке с индуктивностью L заменяют комплек­сом 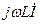. Оператор j, здесь как множитель, указывает на то, что вектор напряжения 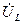повернут на угол +π/2 по отношению к вектору тока 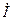. Следовательно, если на комплексной плоскости вектор напряжения U_L направлен по оси действительных значе­ний (оси +1), то вектор тока I направлен по мнимой оси -j. При этом, если вектор U_L занимает любое другое положение на комплексной плоскости, вектор тока I будет занимать по отноше­нию к вектору U_L положение, определяемое углом -π/2.

Значение напряжения 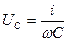на емкостном элементе С заменяют комплексом . Умножение на –j указывает на то, что напряжение на емкости по фазе отстает от тока на угол π/2.

Уравнения электрического состояния в комплексной форме имеют вид: для ветви 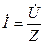; для узла 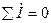; для контура .

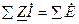Контурное уравнение электрического состояния цепи при последовательном соединении элементов R, L, C, записанное в комплексной форме, имеет вид , откуда можно найти комплекс тока , где 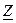- комплексное сопротивление цепи.

Чтобы освободится от мнимых составляющих комплексного числа в знаменателе, умножим и разделим правую часть уравнения на сопряженный комплекс сопротивления: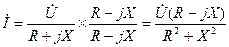

В общем случае комплекс полного сопротивления 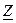в показательной форме состоит из модуля комплекса 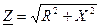и аргумента φ, который определяется разностью углов начальных фаз напряжения (ψ_u) и тока (ψ_i),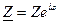

При параллельном соединении приемников (рис. 5.22) они находятся под общим напряжением .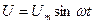

В комплексной форме выражения для тока в неразветвленной части цепи согласно уравнению электрического состояния для узла 1 (или узла 2) имеет вид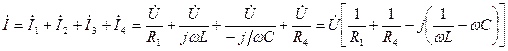

или

Под комплексной проводимостью понимают отношение комплекса тока к комплексу напряжения, или величину, обратную комплексу сопротивления .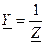

Для нагрузки индуктивного характера, когда X_L>X_C,

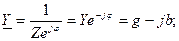
Рис. 5.22

Для нагрузки емкостного характера X_L<X_C,

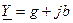
Пользуясь комплексными числами, анализ режимов в электрических цепях при смешанном соединении элементов можно производить рассмотренными ранее методами, например методом эквивалентных преобразований или методом пропорциональных величин.