1. Сложение (вычитание) комплексных чисел.
 ,
,
т. е. при сложении (вычитании) комплексных чисел их действительные и мнимые части складываются (вычитаются).
2. Умножение комплексных чисел.
Комплексные числа перемножаются как двучленны; при этом необходимо учитывать, что
 ,
, 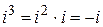 ,
, 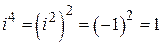 .
.
Умножим два комплексных числа, имеем
 .
.
Получим произведение комплексных чисел в тригонометрическом виде
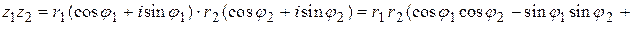
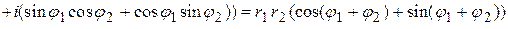 .
.
Следовательно, при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
В частном случае, при умножении двух комплексно-сопряженных чисел получается квадрат их модуля.
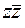
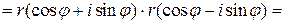
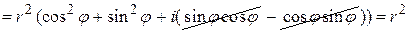 .
.
Следствие. Возведение в степень комплексного числа.
Если  , то
, то
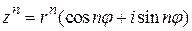 ,
,
т. е. при возведении комплексного числа в n -ю степень его модуль возводится в эту степень, а аргумент умножается на эту степень.
Например 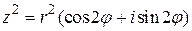 .
.
Запишем в координатном виде 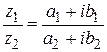 .
.
Умножим числитель и знаменатель на число комплексно-сопряженное знаменателю, получим
 .
.
Более удобный вид частного комплексных чисел получим при использовании тригонометрической записи.
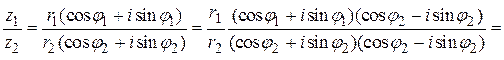

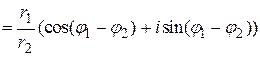 .
.
Следовательно, при делении комплексных чисел их модули делятся, а аргументы вычитаются.
4. Извлечение корня из комплексного числа.
Пусть  , а
, а 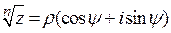 . Равенство
. Равенство
 возведем в n -ю степень, получим
возведем в n -ю степень, получим
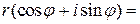

Отсюда получим для модулей чисел равенство
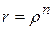 или
или  .
.
Аргументы равных чисел могут отличаться на число, кратное 2p, поэтому для аргументов чисел z и 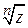 имеем
имеем
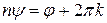 ,
, 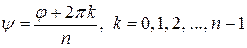 .
.
Следовательно,
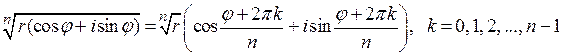 .
.
Корень n -ой степени из действительного числа А, отличного от нуля, имеет n значений, так как действительное число является частным случаем комплексного и может быть представлено в тригонометрической форме: если 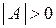 , то
, то 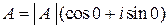 , если
, если 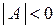 , то
, то 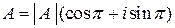 .
.
Пример 7.19. Найти корень кубический из комплексной единицы 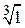 . Представим эту единицу в тригонометрическом виде
. Представим эту единицу в тригонометрическом виде 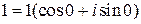 . Получаем
. Получаем
 =
=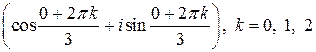 .
.
При 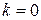 имеем корень
имеем корень 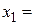
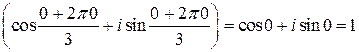 .
.
При  корень
корень 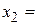
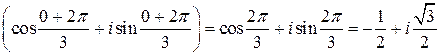 .
.
При 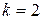 корень
корень
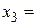
 .
.
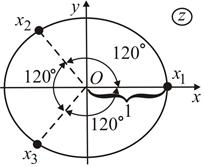 Рис. 84 Рис. 84 | Таким образом, корень кубический из единицы 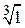 в комплексной плоскости имеет три значения: в комплексной плоскости имеет три значения:  , ,  , , 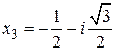 , которые изображены точками на рис. 84. Все корни имеют один и тот же модуль, равный единице, поэтому они располагаются на окружности. Аргументы корней равны: 0°, 120° и 240°, поэтому они делят окружность на три равных части. , которые изображены точками на рис. 84. Все корни имеют один и тот же модуль, равный единице, поэтому они располагаются на окружности. Аргументы корней равны: 0°, 120° и 240°, поэтому они делят окружность на три равных части. |
Пример 7.20. Найти 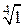 .
.
Получаем 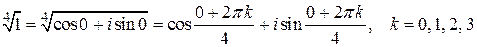 .
.
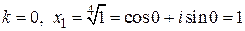 ;
; 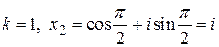 ;
;
 ;
; 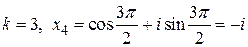 ;
;
Пример 7.21. Решить уравнение  .
.
Находим  .
.
 2014-02-02
2014-02-02 836
836








