2014-02-02
2279
С помощью рангов соответствующих матриц можно определить взаимное расположение подпространств из некоторого пространства. При этом определённую пользу принесёт следующая теорема.
Теорема 7.14 Кронекера-Капели.
Система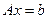 
совместна тогда и только тогда, когда 
.
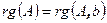Доказательство. Очевидно.
В качестве примера определим взаимное расположение двух линейных многообрази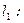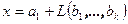й: 
и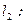 
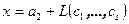(предполагается линейная независимость систем векторов 
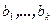и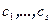 
). Рассмотрим две системы линейных уравнени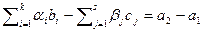й 
и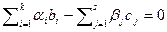 
. Положим 
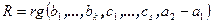и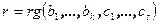 
.
Совместность первой системы означает, что у линейных многообразий есть общая точка. Равенство рангов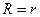 
является необходимым и достаточным условием совместности первой системы линейных уравнений (теорема Кронекера-Капели). Размерность пространства решений второй системы позволяет определить размерность пересечения линейных оболочек 
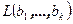и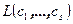 
по формуле 
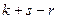. Этой информации достаточно для описания взаимного расположения линейных многообразий. В качестве примера приведём в таблицах все случаи взаимного расположения двух прямых, прямой и плоскости, двух плоскостей.
Две прямые (k=s=1)
| r | R | примечание |
| Прямые совпадают (есть общая точка и размерность пересечения равна 1) | ||
| Прямые параллельны | ||
| Прямые пересекаются в одной точке | ||
| Прямые скрещиваются (нет общих точек и не параллельны) |
Прямая и плоскость (k=1, s=2)
| r | R | примечание |
| Прямая лежит в плоскости | ||
| Прямые параллельна плоскости | ||
| Прямая пересекается с плоскостью в единственной точке | ||
| Прямая и плоскость скрещиваются (нет общих точек и не параллельны) |
Две плоскости (k=s=2)
| r | R | примечание |
| Плоскости совпадают | ||
| Плоскости параллельны | ||
| Плоскости пересекаются по прямой | ||
| Плоскости скрещиваются, но имеют параллельные прямые | ||
| Плоскости пересекаются в единственной точке | ||
| Плоскости абсолютно скрещиваются (ни какие прямые одной плоскости не параллельны прямым другой плоскости) |
