Методы экстраполяции, основаны на прогнозировании поведения или развития объектов в будущем по тенденциям его поведения в прошлом. Применение методов экстраполяции, как правило, не требует моделирования частных параметров объекта и показателей организационно-технического уровня производства. Наиболее распространенными являются методы экстраполяции по математическим моделям и графический (от руки, на глазок). Оба метода требуют наличия информации о прогнозируемом параметре объекта за период в 2 и более раза больше прогнозируемого периода. Для учета изменений качества объекта в прогнозируемом периоде и организационно-технического уровня производства у изготовителя и потребителя объекта применяются корректирующие коэффициенты.
Рассмотрим пример. Допустим, нам необходимо спрогнозировать себестоимость выработки сжатого воздуха в 2000 г. в условиях станкостроительного завода. Воздух на этом заводе сжимается воздушными поршневыми компрессорами типа ВП. На заводе не ведется учет себестоимости выработки сжатого воздуха каждым компрессором, но ведется учет всех элементов затрат по эксплуатации и ремонтам компрессорной станции в целом, а также ее годовой производительности. Поделив сумму годовых затрат по компрессорной станции на годовую производительность (годовой объем сжатого воздуха), получим себестоимость выработки единицы объема сжатого воздуха.
|
|
|
Себестоимость одной тысячи м3 сжатого воздуха на заводе по годам за период с 1992 по 1999 гг. составила соответственно 2,10 у.е.; 2,03; 1,95; 2,02; 1,86; 1,87; 1,83; 1,80 у.е. Нанесем эти данные на график (рис. 5.1).
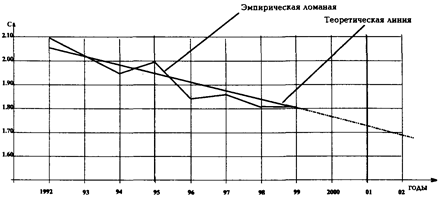
Рис. 5.1. Динамика себестоимости выработки 1 тыс. м3 сжатого воздуха на станкостроительном заводе
По имеющимся данным, себестоимость выработки сжатого воздуха на 2000 г. можно спрогнозировать методом наименьших квадратов на ЭВМ и графически. Для разработки модели прогнозирования по первому методу составляется матрица исходных данных по следующей форме:
| Х | ||||||||
| Y | 2,10 | 2,03 | 1,95 | 2,02 | 1,86 | 1,87 | 1,83 | 1,80 |
В этой таблице X — год (1992 г. — 1, 1993 г. — 2 и т.д.), Y — себестоимость сжатого воздуха, у.е/тыс. м3.
После решения матрицы на ЭВМ по стандартной программе, статистической обработки данных методом наименьших квадратов были получены следующие модели для прогнозирования себестоимости:
Y = 2,10 — 0,0373Х и Y = 2,095 Х–0.059.
Уравнение регрессии по степенной форме зависимости не отвечает требованиям по критерию Фишера: расчетное значение критерия равно 4,26, а табличное — 5. Поэтому было принято уравнение по линейной зависимости, отвечающее требованиям: коэффициент парной корреляции равен 0,78, ошибка аппроксимации ± 1,5%, критерий Стьюдента — 4,68 при табличном, равном 2, критерий Фишера — 4,95.
|
|
|
Подставляя в линейное уравнение регрессии вместо Х соответствующую цифру (1 — для 1992 г., 2 — 1993, 7 — 1998, 8 — 1999 г.), получим следующие теоретические или расчетные значения себестоимости:
Y1992 = 2.10 – 0.0373·1 = 2,06,
Y1998 = 2.10 – 0.0373·7 = 1,86,
Y1999 = 2.10 – 0.0373· 8 = 1,80.
По полученным точкам построим теоретическую линию снижения себестоимости выработки сжатого воздуха в условиях данного завода. Участок от 2000 до 2002 г. является прогностическим, и он обозначен пунктирной линией. За год в среднем себестоимость снижается на 1,8%.
Линию снижения себестоимости можно построить также графически, без нахождения математической модели, на глазок. Однако он по сравнению с предыдущим менее точен, рекомендуется только для предварительного определения тенденции изменения функции.
В этом примере корректирующие коэффициенты не учтены, так как до 2002 года на анализируемом заводе не намечаются изменения организационно-технических факторов производства сжатого воздуха. Также не учтена инфляция.
Вопрос 3. Параметрические методы
Параметрические методы прогнозирования полезного эффекта и затрат, основанные на установлении зависимостей между параметрами объекта и организационно-технического уровня производства, с одной стороны, и полезным эффектом или элементом затрат — с другой.
Параметрические методы прогнозирования подразделяются на два вида: по удельным показателям и по уравнениям регрессии.
Для установления уравнений регрессии необходимо, чтобы количество статистических данных было не менее чем в три раза больше количества факторов (см. табл. 4.3). По объектам, не отвечающим этим требованиям, полезный эффект или затраты рекомендуется определять по удельным показателям. Например, полезный эффект объекта рассчитывается по формуле
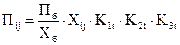 (5.1)
(5.1)
где Пit — полезный эффект объекта в j-x условиях эксплуатации в t-м году;
Пб — среднегодовой полезный эффект базового объекта, аналогичного проектируемому;
Xб — важнейшая характеристика (главная функция) базового объекта, например, часовая производительность и т. п.;
Xjt — важнейшая характеристика проектируемого объекта в j-x условиях эксплуатации в t- м прогнозируемом году;
K1t — коэффициент, учитывающий повышение надежности проектируемого объекта по сравнению с базовым на t-й год;
K2t — коэффициент, учитывающий изменение организационно-технического уровня производства у потребителей проектируемого объекта в t-м году эксплуатации по сравнению с уровнем производства у потребителей базового объекта;
K3t — коэффициент, учитывающий изменение организационно-технического уровня производства у ремонтной организации объекта в t-м году по сравнению с базовым периодом.
Количество корректирующих коэффициентов можно увеличить.
По аналогичной схеме определяются и элементы затрат по стадиям жизненного цикла проектируемого объекта. Например, затраты на освоение производства проектируемого объекта можно определить по формуле
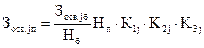 (5.2)
(5.2)
где Зосв.jп — затраты на освоение проектируемого объекта на j-м предприятии;
Зосв.jб — то же базового объекта;
Hб и Нп — соответственно количество наименований деталей (без крепежных деталей) в базовом и проектируемом объекте;
К1j — коэффициент, учитывающий изменение показателя технологической оснащенности проектируемого объекта на j-м предприятии по сравнению с базовым объектом;
K2j — коэффициент, учитывающий изменение показателя освоенности деталей проектируемого объекта по сравнению с базовым объектом;
К3j — коэффициент, учитывающий повышение сложности проектируемого объекта по сравнению с базовым.
Коэффициенты определяются отношением соответствующего показателя по проектируемому объекту к показателю по базовому объекту. Например, коэффициент, учитывающий изменение показателя технологической оснащенности объекта, определяется по формуле
|
|
|
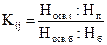 (5.3)
(5.3)
где Носв.t — количество наименований технологической оснастки, необходимой для изготовления проектируемого объекта;
Носв.б — то же базового объекта.
Затраты на изготовление объекта с применением метода удельных показателей на ранних стадиях его проектирования определяется по формуле
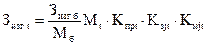 (5.4)
(5.4)
где Зизг.t — затраты на изготовление проектируемого объекта на j-м предприятии в t-м году;
Зизг.б — затраты на изготовление базового объекта;
Мб и Мt — соответственно масса базового и проектируемого объекта;
Кпрt — коэффициент, учитывающий закономерность неуклонного роста производительности труда, на t-й год;
Kмjt — коэффициент, учитывающий влияние на затраты по изготовлению масштаба выпуска проектируемого объекта по сравнению с масштабом выпуска базового объекта на j-м предприятии в t-м году.
Затраты на обращение определяются индивидуально для каждого объекта. Например, затраты на транспортирование, хранение и монтаж компрессорного оборудования укрупненно можно принять равными 10% от его цены. Для некоторых объектов, кроме того, необходимо строить здания для монтажа (например, для автомобиля — гараж), ремонтную базу. Эти затраты можно определить только путем составления соответствующих смет.
Затраты на эксплуатацию проектируемого объекта по методу удельных показателей можно определить по формуле
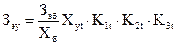 (5.5)
(5.5)
где Зэу — затраты на эксплуатацию проектируемого объекта в у-х условиях в t-м году;
Зэб — среднегодовые затраты по эксплуатации базового объекта.
4. Экспертные методы
При прогнозирования полезного эффекта и элементов затрат по объектам, которые не характеризуются одной главной функцией, или не имеется достаточное количество статистических данных (в три раза больше количества показателей объекта). рекомендуется использовать экспертные методы. Сущность экспертных методов прогнозирования заключается в выработке коллективного мнения группы специалистов в данной области. Существует несколько различных методов экспертной оценки развития объекта в будущем. Рассмотрим здесь только один метод — метод баллов, который можно применять для прогнозирования как полезного эффекта объекта, так и элементов затрат.
|
|
|
Сначала формируется экспертная группа из специалистов в данной области, численность которой должна быть равна или больше 9. Для повышения однородности состава группы путем анонимного анкетирования можно сделать отсев специалистов, которые, по мнению большинства, не совсем компетентны в данной области.
Затем коллективно устанавливаются или выбираются несколько важнейших параметров (3—5) объекта, влияющих на полезный эффект и элементы затрат.
Следующий шаг — установление важности параметра экспертным путем. Рассмотрим два метода. По первому — каждый эксперт каждому параметру объекта присваивает баллы по шкале от 0 до 10. Тогда важность параметра объекта в баллах определяется по формуле:
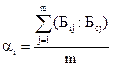 (5.6)
(5.6)
где 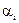 — весомость i-го параметра объекта;
— весомость i-го параметра объекта;
i — номер параметра объекта;
j — номер экcперта;
m — количество экспертов в группе;
Бij — балл, присвоенный i-му параметру j-м экспертом;
Бcj — сумма баллов, присвоенных j-м экспертом всем параметрам объекта.
Допустим, экспертная группа установила, что объект характеризуется четырьмя важнейшими параметрами (главными функциями). Эта группа состоит из 9 специалистов в данной области. Первый эксперт присвоил параметрам следующие баллы: первому параметру — 7 баллов, второму — 6 баллов, третьему — 2, четвертому — 5. Второй эксперт этим параметрам присвоил соответственно следующие баллы: 6,8,4,4 и т.д. Сумма баллов у экспертов получилась следующая: у первого эксперта — 20 (7+6+2+5), второго — 22 и далее соответственно 19,25,21,20,24,23. Первому параметру эксперты присвоили следующие баллы: 7,8,6,7,8,6 и 7. Тогда весомость первого параметра будет равна
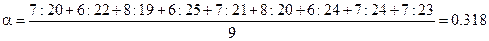
Аналогично определяется весомость и других параметров объекта. Весомость параметров рекомендуется определять по следующей методике.* Сначала каждый эксперт находит соотношение между параметрами попарно. Если весомость данного параметра, по мнению эксперта, выше другого, с которым сравнивается данный параметр, ему присваивается два балла. Если весомость параметров одинакова, данному параметру присваивается один балл. И если весомость данного параметра ниже другого, то первому параметру баллов не дается.
Допустим, что 9 экспертов четырем параметрам объекта присвоили следующие баллы (табл. 5.2).
Средняя оценка определяется делением суммы баллов на количество экспертов. По средним оценкам рассчитывается весомость параметров (табл. 5.3).
В табл. 5.3 значения соотношений параметров, которые отсутствуют в табл. 5.2, определены путем вычитания из второго значения обратного соотношения из табл. 5.2. Например, в табл. 5.2 отсутствует соотношение параметров Х2 и X1 имеется соотношение обратное X1 и Х2, равное 1,2. Тогда соотношение Х2 и X1 будет обратно и равно 0,8 (2 — 1,2). Весомость параметров определяется экспертным методом по объектам, характеризующимся несколькими важнейшими параметрами разной размерности. Для того, чтобы сложить (условно) подобные параметры и определить полезный эффект и элементы затрат по объекту, рекомендуется применять систему баллов.
Таблица 5.2
Результаты экспертной оценки
| Соотношение параметров | Эксперты | Сумма баллов | Средняя оценка | ||||||||
| Х1 и Х2 | 1,2 | ||||||||||
| Х1 и Х3 | 1,8 | ||||||||||
| X1 и Х4 | 1,4 | ||||||||||
| Х2 и Х3 | 1,3 | ||||||||||
| Х2 и Х4 | 1,1 | ||||||||||
| ХзИХ4 | 0,9 |
Таблица 5.3
Весомость параметров (а)
| Параметры | X1 | Х2 | Х3 | Х4 | а |
| X1 | 1,0 | 1,2 | 1,8 | 1,4 | 5,4 |
| Х2 | 0,8 | 1,0 | 1,3 | 1,1 | 4,2 |
| Х3 | 0,2 | 0,7 | 1,0 | 0,9 | 2,8 |
| Х4 | 0,6 | 0,9 | 1,1 | 1,0 | 3,6 |
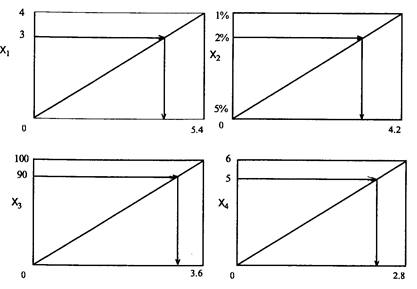
Система баллов строится следующим образом. Допустим,что установленные в табл. 5.3 весомости параметров характерны для группы приборов одного назначения: X1 — количество измеряемых параметров, Х2 — точность измерений, %, Х3 — пределы измерений основного параметра, Х4 — количество измерений в единицу времени. Максимальные значения параметров для данной группы приборов следующие: X1 — 4, Х2 — ± 5%, Х3 — 100 и Х4 — 6 измерений в минуту. По этим значениям параметров и их весомости (см. табл. 5.3) строится система баллов для прогнозирования полезного эффекта новых приборов данного класса (рис. 5.2).
При построении данной системы баллов для упрощения принято, что зависимость между параметрами и полезным эффектом или элементами затрат прямо пропорциональная (линейная). При необходимости уточнения системы баллов можно построить и криволинейные зависимости.
 2014-02-02
2014-02-02 1178
1178
