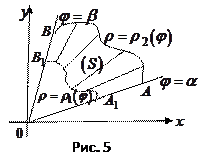 1). Полярной системой координат удобно пользоваться, если область интегрирования ограничена окружностью или линией
1). Полярной системой координат удобно пользоваться, если область интегрирования ограничена окружностью или линией 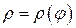 , или линией, уравнение которой содержит
, или линией, уравнение которой содержит 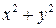 .
.
2). Если уравнение линии, ограничивающей область, или подынтегральная функция содержат 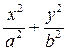 , то удобно перейти к обобщенным полярным координатам
, то удобно перейти к обобщенным полярным координатам
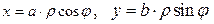 ; тогда
; тогда 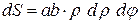 .
.
Пример 1. Вычислить площадь фигуры, ограниченной линией 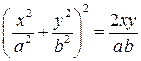 .
.
Решение. Сначала построим линию, исследуя ее уравнение. Выражение 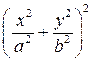 неотрицательно, значит, и
неотрицательно, значит, и 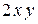 неотрицательно, т.е. линия находится в первой и третьей четвертях. Уравнение линии не изменится при замене
неотрицательно, т.е. линия находится в первой и третьей четвертях. Уравнение линии не изменится при замене  на
на 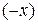 и
и 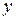 на
на 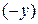 . Значит, эта линия симметрична относительно начала координат и ее достаточно построить в первой четверти, а затем воспользоваться симметрией.
. Значит, эта линия симметрична относительно начала координат и ее достаточно построить в первой четверти, а затем воспользоваться симметрией.
Наличие в уравнении линии выражения 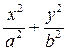 наводит на мысль воспользоваться обобщенными полярными координатами
наводит на мысль воспользоваться обобщенными полярными координатами 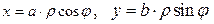 .
.
Тогда 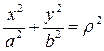 и уравнение линии примет вид
и уравнение линии примет вид
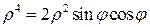 , или
, или 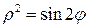 , или
, или 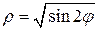 .
.
Как отмечалось, достаточно сначала построить линию в первой четверти, т.е. для 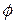 , принадлежащих отрезку
, принадлежащих отрезку 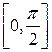 . Для этого составим следующую таблицу:
. Для этого составим следующую таблицу:
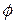 | 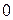 | 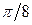 | 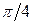 | 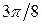 | 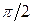 |
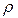 | 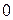 | 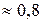 | 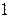 | 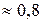 | 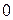 |
 Построим точки с вычисленными координатами
Построим точки с вычисленными координатами 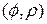 , соединим их плавной линией, которую затем, воспользовавшись свойством симметрии, отобразим зеркально относительно начала координат (рис. 6). Вычислим площадь
, соединим их плавной линией, которую затем, воспользовавшись свойством симметрии, отобразим зеркально относительно начала координат (рис. 6). Вычислим площадь 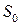 той части фигуры, которая расположена в первой четверти:
той части фигуры, которая расположена в первой четверти:
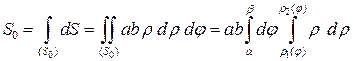 .
.
Чтобы расставить внутренние пределы интегрирования, т.е. пределы изменения 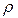 , будем двигаться в области
, будем двигаться в области 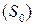 по лучам, выходящим из полюса. На каждом таком луче
по лучам, выходящим из полюса. На каждом таком луче 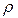 меняется от значения
меняется от значения 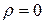 в точке 0 до значения
в точке 0 до значения 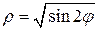 на линии, ограничивающей область
на линии, ограничивающей область 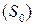 . Кроме того, эта область заключена между лучами
. Кроме того, эта область заключена между лучами 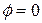 и
и 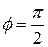 . Поэтому
. Поэтому 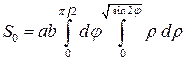 .
.
Вычислим повторный интеграл, начиная с вычисления внутреннего интеграла
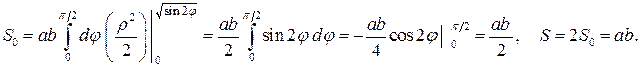
Пример 2. Доказать, что 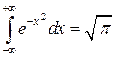 .
.
Решение. Вычислим вспомогательный интеграл 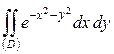 для двух областей:
для двух областей:
а) если  круг
круг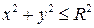 , то, переходя к полярным координатам, получим
, то, переходя к полярным координатам, получим
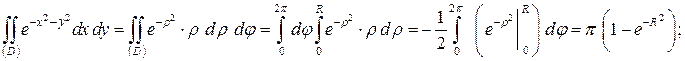
при 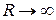 область
область 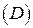 , расширяясь, заполнит всю плоскость (обозначим ее
, расширяясь, заполнит всю плоскость (обозначим ее 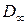 ) и
) и

б) если  квадрат
квадрат 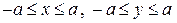 , то
, то
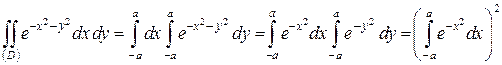 ;
;
при 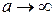 область
область 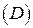 , расширяясь, опять заполнит всю плоскость (
, расширяясь, опять заполнит всю плоскость (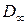 ) и
) и
 .
.
Итак, 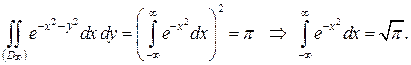
 2014-02-02
2014-02-02 837
837








