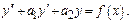
Общее реш-е ДУ имеет вид 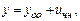 где
где 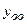 - общее реш-е однородного ур-я,
- общее реш-е однородного ур-я, 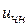 - частное реш-е неоднородного ур-я или
- частное реш-е неоднородного ур-я или
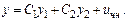
Найдем 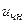 . Рассмотрим частные случаи.
. Рассмотрим частные случаи.
I) Правая часть имеет вид 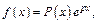 где
где 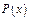 - многочлен
- многочлен 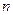 -й степени. Реш-е
-й степени. Реш-е 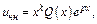 где:
где: 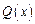 - многочлен той же степени, что и
- многочлен той же степени, что и 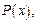
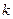 - кратность
- кратность 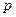 среди корней характеристического ур-я (если такого корня нет, то
среди корней характеристического ур-я (если такого корня нет, то 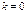 ).
).
Коэф-ты многочлена 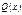 находим методом неопределенных коэф-в.
находим методом неопределенных коэф-в.
Частные случаи:
а) 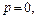
б) 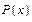 - многочлен нулевой степени.
- многочлен нулевой степени.
Примеры: 1) 
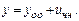
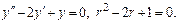
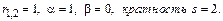
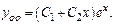
Характеристики правой части: 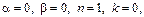 т.к. среди корней характеристич-го ур-я нет корня с такими же характ-ками.
т.к. среди корней характеристич-го ур-я нет корня с такими же характ-ками.
Частное реш-е неоднородного ур-я имеет вид 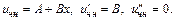 Подставим в ДУ
Подставим в ДУ 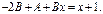
Применим метод неопределенных коэф-в:

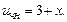
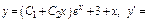
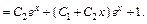 Из нач-х усл-й
Из нач-х усл-й
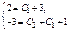
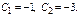
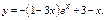
2) 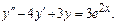
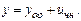
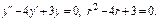
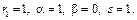
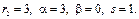
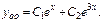 Характеристики правой части:
Характеристики правой части: 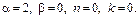
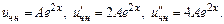
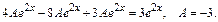
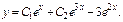
3) 
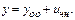
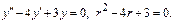
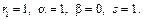
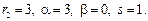
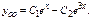 Характеристики правой части:
Характеристики правой части: 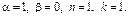
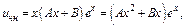
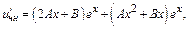
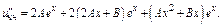
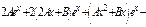
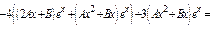
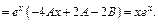
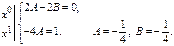
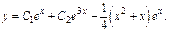
II) Правая часть имеет вид 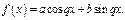
а) Если 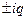 не явл-ся корнями характеристического ур-я, то
не явл-ся корнями характеристического ур-я, то 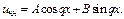 (*)
(*)
б) Если 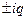 корни характеристического ур-я, то
корни характеристического ур-я, то 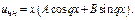 (**)
(**)
В частном случае, когда  или
или 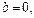 частное реш-е все равно имеет вид (*) или (**).
частное реш-е все равно имеет вид (*) или (**).
Примеры: 1) 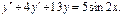
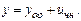
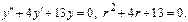
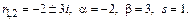
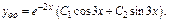
Характеристики правой части: 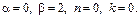
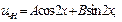
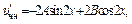
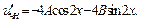
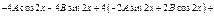
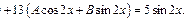
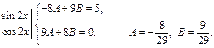
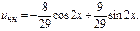
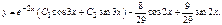
2) 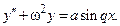
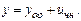
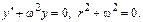

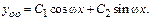
а)  Характеристики правой части:
Характеристики правой части: 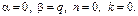
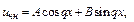
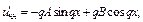
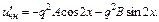
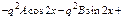
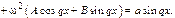
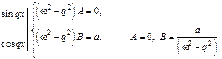
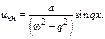
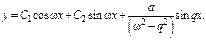
б)  Характеристики правой части:
Характеристики правой части: 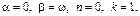
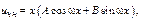
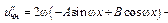
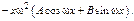
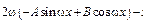
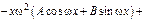

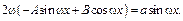
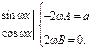
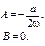
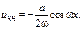
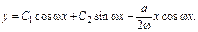
III) Правая часть имеет вид 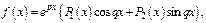
где 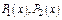 - многочлены степени
- многочлены степени 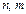 соотв-но.
соотв-но.  Возможны два случая.
Возможны два случая.
а)  - не есть корни характеристического ур-я. Тогда частное реш-е неоднородного ур-я имеет вид
- не есть корни характеристического ур-я. Тогда частное реш-е неоднородного ур-я имеет вид 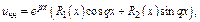 где
где  - многочлены степени
- многочлены степени 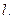
б) 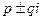 - корни характеристического ур-я. Тогда частное реш-е неоднородного ур-я имеет вид
- корни характеристического ур-я. Тогда частное реш-е неоднородного ур-я имеет вид 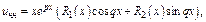 где
где 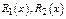 - многочлены степени
- многочлены степени 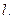
Случай (I) получается, если  случай (II) получается, если
случай (II) получается, если 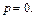 Степени многочленов
Степени многочленов 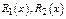 могут получиться меньше
могут получиться меньше 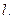
Пример. 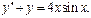

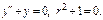
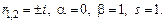

Характеристики правой части: 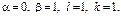
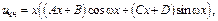
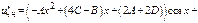
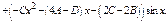

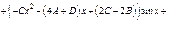
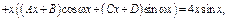
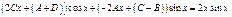
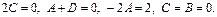
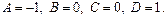
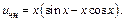
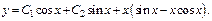
Теорема. Пусть правая часть ДУ 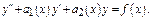 равна сумме двух ф-й
равна сумме двух ф-й 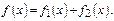 Пусть
Пусть  - частное реш-е при
- частное реш-е при 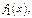
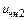 - частное реш-е при
- частное реш-е при 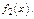 Тогда
Тогда 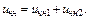
Док-во. 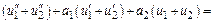
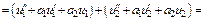
 2014-02-02
2014-02-02 328
328








