Интегралы типа 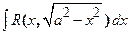 ,
, 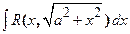 ,
, 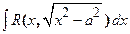 приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью тригонометрических подстановок:
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью тригонометрических подстановок: 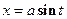 для первого интеграла;
для первого интеграла; 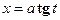 для второго интеграла;
для второго интеграла; 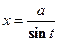 для третьего интеграла.
для третьего интеграла.
5. Интегралы типа 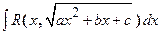 , где
, где 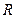 – рациональная функция относительно x и
– рациональная функция относительно x и 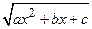 .
.
Один из возможных методов интегрирования состоит в следующем.
Выделяем полный квадрат в квадратном трехчлене 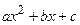 и совершаем замену переменной по формуле
и совершаем замену переменной по формуле 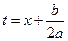 , после этого исходный интеграл сводится к одному из следующих трех типов:
, после этого исходный интеграл сводится к одному из следующих трех типов:
1. 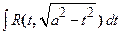 ;
;
2. 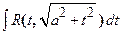 ;
;
3. 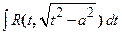 .
.
Эти три типа интегралов вычисляются с помощью тригонометрической подстановки соответственно.
1) 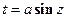 ,
,
2) 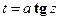 ,
,
3) 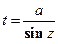 .
.
В результате этих подстановок указанные интегралы приводятся к виду 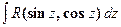 или
или 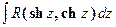 .
.
В частном случае, когда требуется вычислить интегралы типа 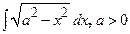 и
и 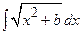 , можно обойтись без замены переменной. Вычислим первый из них:
, можно обойтись без замены переменной. Вычислим первый из них:
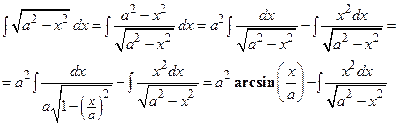 .
.
Для вычисления последнего интеграла воспользуемся методом интегрирования по частям: 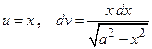 .
.
Тогда 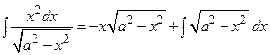 .
.
Вернемся к исходному интегралу: 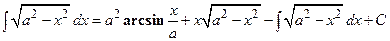 .
.
Из последнего равенства получаем 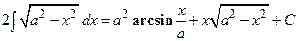 , и, разделив обе части на два, найдем
, и, разделив обе части на два, найдем 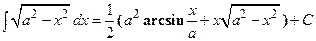 .
.
Поступая аналогично для 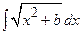 , получим
, получим 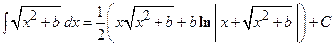 .
.
Замечание. Интеграл типа 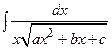 целесообразно находить с помощью подстановки
целесообразно находить с помощью подстановки 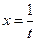 .
.
 2014-02-02
2014-02-02 1633
1633







