Предположим, что имеется выборка объема 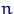 , элементы которой
, элементы которой 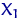 ,
,  ,
, 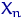 независимы, одинаково распределены и имеют распределение
независимы, одинаково распределены и имеют распределение  , известным образом зависящее от неизвестного параметра
, известным образом зависящее от неизвестного параметра  .
.
Здесь  — некий класс распределений, целиком определяющихся значением скалярного или векторного параметра
— некий класс распределений, целиком определяющихся значением скалярного или векторного параметра  . Параметр
. Параметр  принимает значения из некоторого множества
принимает значения из некоторого множества  .
.
Например, для всех 
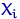 имеют распределение Пуассона
имеют распределение Пуассона  , где
, где 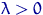 — неизвестный параметр; здесь
— неизвестный параметр; здесь 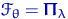 ,
,  ,
,  ;
; 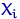 имеют распределение Бернулли
имеют распределение Бернулли 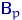 , где
, где 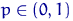 — неизвестный параметр; здесь
— неизвестный параметр; здесь 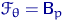 ,
, 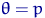 ,
, 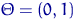 ;
; 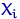 имеют равномерное распределение
имеют равномерное распределение 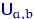 , где
, где 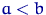 — неизвестные параметры; здесь
— неизвестные параметры; здесь 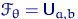 ,
, 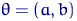 ,
, 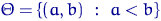 ;
; 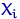 имеют равномерное распределение
имеют равномерное распределение 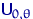 , где
, где  — неизвестный параметр; здесь
— неизвестный параметр; здесь 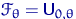 ,
,  ;
; 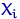 имеют нормальное распределение
имеют нормальное распределение  , где
, где 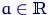 ,
, 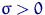 — неизвестные параметры; здесь
— неизвестные параметры; здесь 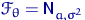 ,
, 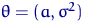 ,
, 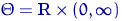 ;
; 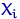 имеют нормальное распределение
имеют нормальное распределение 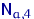 , где
, где 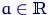 — неизвестный параметр; здесь
— неизвестный параметр; здесь 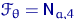 ,
, 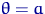 ,
, 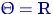 .
.
Такая постановка имеет смысл, поскольку редко о проводимом эксперименте совсем ничего нельзя сказать. Обычно тип распределения ясен заранее, и требуется лишь указать значения параметров этого распределения.
Так, в широких предположениях рост юношей одного возраста имеет нормальное распределение (с неизвестными средним и дисперсией), а число покупателей в магазине в течение часа (не часа пик) — распределение Пуассона, и опять-таки с неизвестной «интенсивностью» 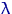 .
.
 2014-02-02
2014-02-02 1839
1839
