Понятие передаточных функций и частотных характеристик

Для оценки свойств элемента или системы Лаплас ввел понятие передаточной функции. Передаточной функцией называется отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.

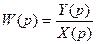. (5)

Понятием передаточной функции удобно пользоваться при математическом описании и расчёте процессов изменяющихся во времени.

При анализе процессов удобно пользоваться понятием частотной передаточной функции.

Частотная передаточная функция формально получается из (5) путём подстановки вместо р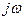

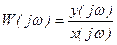. (6)

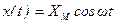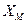Здесь предполагается, что на вход подаётся гармонический сигнал , где - амплитуда, а ω – угловая частота внешнего воздействия.

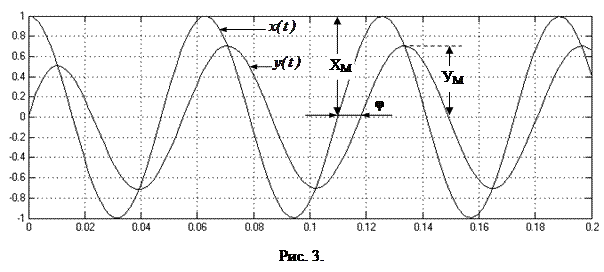
Выходная переменная в установившемся режиме 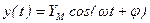изменяется с той же угловой частотой, но, в общем случае, уже с другой амплитудой 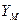и с определённым фазовым сдвигом на угол 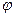относительно входной переменной (рис. 3).

Пример 1. Допустим, что объект описывается дифференциальным уравнением

.

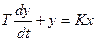Переходя к операторной форме записи, получим 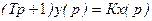. Здесь символ дифференцирования заменён оператором р, а переменные рассматриваются в виде изображений по Лапласу. Из полученного выражения вводится понятие передаточной функции

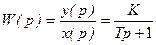. (7)

Принимая 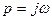, получаем выражение для частотной передаточной функции

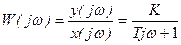. (8)

Полученное выражение представляет собой уже комплексное число, которое можно изобразить на комплексной плоскости. Комплекс – это вектор, который характеризуется амплитудой, действительной и мнимой частью, или угловым сдвигом относительно комплексной плоскости.

Умножая числитель и знаменатель на сопряжённый комплекс, получим

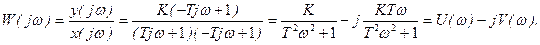(9)

Здесь введены обозначения:

- вещественная составляющая комплексной функции ,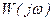

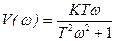- мнимая составляющая комплексной функции .

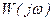Выражение (9) можно представить в другой форме записи

,

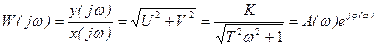где - амплитудная частотная характеристика (АЧХ),

- фазовая частотная характеристика (ФЧХ).

Таким образом, частотная передаточная функция – это комплексная функция. Эту функцию можно рассматривать как в полярной, так и в декартовой системе координат

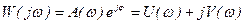. (10)

При решении задач ТАУ удобно рассматривать АЧХ и ФЧХ в логарифмическом масштабе. Прологарифмируем (10)

lnW(јω)= lnA(ω)+ jφ(ω). (11)

Это комплексное выражение, содержащее действительную и мнимую часть. Действительная часть lnA(ω) - характеризует поведение амплитуды, а мнимая jφ(ω) – фазы выходной переменной.

Для практических целей удобнее пользоваться не натуральными, а десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ).

Для построения ЛАЧХ принимается выражение

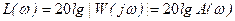(дБ).

Эта величина выражается в децибелах ([1] с. 65-67). Угловая частота (ω) представляется в логарифмическом масштабе.

В настоящее время задачи ТАУ решаются на компьютере с помощью программных комплексов.

Допустим, что нужно рассчитать АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ для звена с передаточной функцией (7)

,

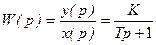где 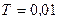с, К= 10.

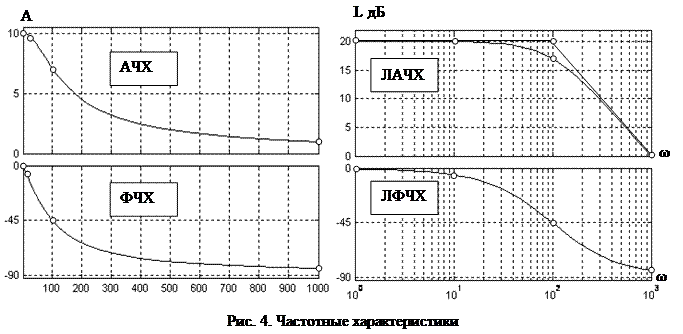
Частотные характеристики (рис. 4) отражают свойства этого звена в частотной области. Расчёт выполнялся с помощью системы Matlab.

4. Типовые динамические звенья

Типовые динамические звенья – это звенья, которые описываются дифференциальными уравнениями не выше второго порядка.

№	Тип	Передаточная функция
	Безынерционное
	Интегрирующее
	Инерционное
	Колебательное
	Дифференцирующее идеальное
	Дифференцирующее реальное
	ПИ - звено