Любое характеристическое уравнение III-го порядка приводится к виду:
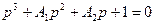
 |
Частотные методы базируются на прямом и обратном преобразовании Фурье.
 Если f(t) – функция периодическая, то для нее применимо:
Если f(t) – функция периодическая, то для нее применимо:
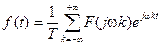
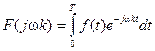
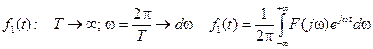
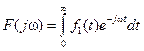
Будем рассматривать: 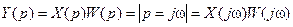
Y(t)=h(t); x(t)=1(t)
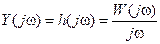
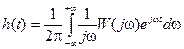
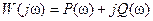 ,
, 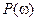 - вещественная характеристика
- вещественная характеристика
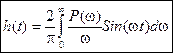
Прямые методы оценки показателя качесва системы основываются на построении переходного процесса в зависимости от 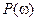 с помощью специальных методов.
с помощью специальных методов.
Косвенные методы позволяют по виду 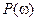 приближенно оценить переходный процесс h(t).
приближенно оценить переходный процесс h(t).
Косвенные оценки 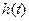 по виду
по виду 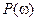

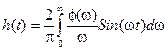 ;
; 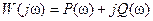 ;
; 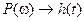
 |  |  | |||
Основные свойства косвенной оценки переходного процесса 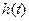 по виду
по виду 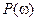
1. Близким вещественным характеристикам соответствуют близкие переходные характеристики 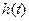 .
.
2. При исследовании вещественной характеристики 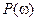 ограничиваются исследованием спектра частот
ограничиваются исследованием спектра частот 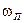 , поскольку при частотах больших
, поскольку при частотах больших 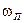 , вещественная характеристика
, вещественная характеристика 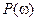 определяет начало переходной характеристики
определяет начало переходной характеристики 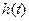 .
.
3. 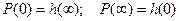
4. Вещественным характеристикам, охватывающим большую площадь соответствует более быстрый переходный процесс (чем шире 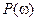 , тем меньше время переходного процесса).
, тем меньше время переходного процесса).
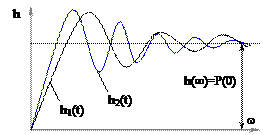

5. 
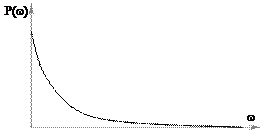 Если
Если 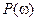 - положительно убывающая функция, то переходная характеристика имеет апериодический характер:
- положительно убывающая функция, то переходная характеристика имеет апериодический характер:  перерегулирование
перерегулирование 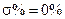
6.
 |
 Если
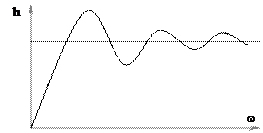
Если 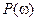 - положительно невозрастающая функция, то переходная характеристика имеет вид затухающих колебаний:
- положительно невозрастающая функция, то переходная характеристика имеет вид затухающих колебаний: 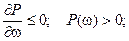 перерегулирование
перерегулирование 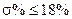
7.
 |
Если вещественная характеристика имеет явно выраженный max, то переходная характеристика будет иметь вид затухающих колебаний и перерегулирование
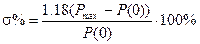
8. Чем выше 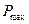 , тем больше амплитуда в переходной характеристике
, тем больше амплитуда в переходной характеристике 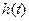 .
.
9. Характер переходного процесса может быть определен по формуле:
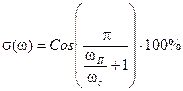
10. Для монотонных процессов: 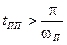 , для?????????? процессов:
, для?????????? процессов: 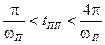 .
.
11. 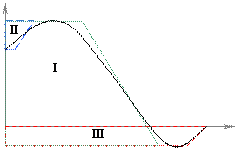 Если вещественную характеристику можно разложить на ряд трапеций, то по параметрам трапеций можно определить перерегулирование
Если вещественную характеристику можно разложить на ряд трапеций, то по параметрам трапеций можно определить перерегулирование 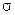 . Все трапеции должны быть прямоугольные:
. Все трапеции должны быть прямоугольные:
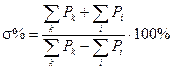 ,
,
где 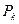 - значение высоты трапеции, имеющей на осях
- значение высоты трапеции, имеющей на осях 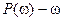 - положительное значение,
- положительное значение, 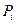 - значение высоты трапеции, имеющей на осях
- значение высоты трапеции, имеющей на осях 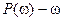 - отрицательное значение.
- отрицательное значение.
 2014-02-02
2014-02-02 1013
1013







