Получение матрицы перехода по схеме переменных состояния

Получение матрицы перехода разложением в ряд

Аналитический способ получения матрицы перехода

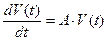(1)

Применим к уравнению (1) преобразование Лапласа:

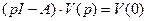, где

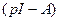- квадратная матрица;

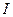- единичная матрица

	Ф(Т)

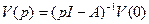
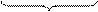
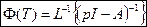
Пример: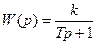

; ;

;

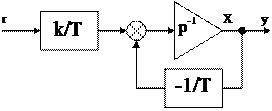
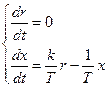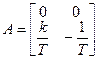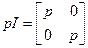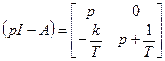
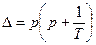
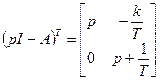
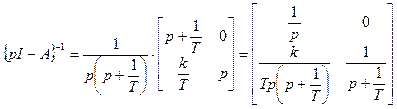
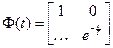
Решением дифференциального уравнения (1) является:

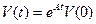
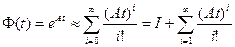
Вычислять до тех пор, пока: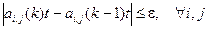

,

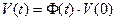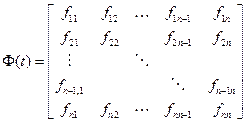
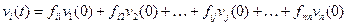
Предположим, что ;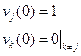

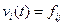
Элемент 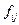, матрицы перехода Ф определяется по схеме переменных состояния как реакция i-й переменной на ед. ступеньку, поданную на j-ю переменную при прочих нулевых начальных условиях.

С точки зрения использования различных способов получения Ф(Т), предпочтение отдается аналитическому способу и способу разложения в ряд, при этом аналитический способ дает явную формулу определения матрицы перехода, что позволяет использовать данную матрицу при различных значениях.

Если величина t является фиксированной, то удобнее использовать метод разложения в ряд, как наиболее экономичный