Пусть материальная точка М движется прямолинейно по закону S = f (t). Как уже известно, производная 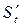 равна скорости точки в данный момент времени:
равна скорости точки в данный момент времени: 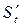 = V.
= V.
Покажем, что вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т. е. 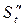 = а.
= а.
Пусть в момент времени t скорость точки равна V, а в момент t + ∆ t — скорость равна V + ∆ V, т. е. за промежуток времени ∆ t скорость изменилась на величину ∆ V.
Отношение 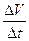 выражает среднее ускорение движения точки за время ∆ t. Предел этого отношения при ∆ t → 0 называется ускорением точки М
выражает среднее ускорение движения точки за время ∆ t. Предел этого отношения при ∆ t → 0 называется ускорением точки М
в данный момент t и обозначается буквой a: 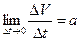 , т. е. V ′ = а.
, т. е. V ′ = а.
Но V = 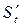 . Поэтому а =
. Поэтому а = 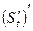 , т. е. а =
, т. е. а = 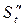 .
.
 2014-02-03
2014-02-03 1462
1462








