Частные случаи

При, например, снижении частоты вращения муфта смещается вниз, и рычаг бав поворачивается относительно точки б, которая в этот момент является мгновенным центром вращения. Золотник, как и точка а, перемещается вниз, открывая доступ силового масла в нижнюю полость сервомотора и сообщая его верхнюю полость со сливом. Поршень идёт вверх на увеличение топливоподачи.

Рис.2.4. Регулятор с жёсткой обратной связью.

САР должна быть как можно менее чувствительной к действию возмущений. Это означает, что при действии возмущений регулируемая величина должна как можно меньше отклоняться от её требуемого (заданного) значения.

Математический аппарат теории автоматического регулирования.

Основной математический аппарат – это дифференциальные уравнения для непрерывных систем и разностные уравнения для дискретных систем. Для первых в общем случае математическое описание, связывающее регулируемую величину с возмущающим и управляющим воздействиями, содержит указанные функции и их производные и имеет вид

F(y, y', y '', … y ⁽ⁿ⁾, z, z', z'', … z^(m), u, u', u'', … u^(s), t) = 0.

Во многих случаях применением корректных упрощений приходят к описанию системы в форме линейного дифференциального уравнения вида

_{n m s}

å a _i y ⁽ⁱ⁾ = å b _j z ^(j) + å c _k u ^(k),

^{i=0 j=0 k=0}

в котором коэффициенты а, в, с могут быть либо функциями времени, либо постоянными величинами. Структура разностных уравнений аналогична.

1.7. Задачи теории автоматического регулирования.

С помощью методов ТАР решаются две основные задачи: задача анализа САР и задача синтеза САР. В задаче анализа известны математическое описание САР и законы изменения во времени возмущающих и управляющих воздействий. Требуется найти закон изменения во времени регулируемой величины. В задаче синтеза известны законы изменения во времени возмущающих и управляющих воздействий и требования к поведению регулируемой величины. В ряде случаев известно также математическое описание объекта регулирования. Требуется найти математическое описание регулятора с целью его технической реализации (построения, настройки и эксплуатации). Очевидно, что вторая задача значительно сложнее первой уже в силу своей неоднозначности, поскольку одинаковое поведение регулируемой величины может быть обеспечено различными регуляторами.

1.8. Требования к системам автоматического регулирования.

С чисто теоретических позиций требования к САР сводятся к требованиям точности соответствия фактического значения регулируемой величины её требуемому (заданному) значению во всех возможных условиях работы. В общей форме эти требования таковы.

2.САР должна как можно лучше реагировать на управляющее воздействие. Это значит, что при поступлении на неё сигналов управления она должна обеспечить быстрый и точный переход регулируемой величины к новому заданному значению.

Очень часто одновременное удовлетворение этих требований либо весьма затруднительно, либо вообще невозможно. Поэтому нередко приходится принимать определённые компромиссные решения.

1.9. Режимы работы САР.

Система автоматического регулирования может находиться в одном из двух режимов работы: статическом либо динамическом.

Статический, или установившийся, режим имеет место тогда, когда воздействия на систему (как возмущающие, так и управляющие) не изменяются во времени. При этом на объекте регулирования наблюдается равенство подвода и отвода энергии либо вещества, обусловливающее неизменность во времени регулируемой величины. Типичный пример – работа САР частоты вращения вала главного судового двигателя при движении в штилевых условиях и неизменном положении органов управления. Частота вращения вала при этом постоянна.

Свойства САР в статике принято иллюстрировать с помощью статических характеристик. Это зависимости регулируемой величины от возмущения (статическая характеристика режима возмущения) и от управляющего воздействия (статическая характеристика режима управления), снятые на различных установившихся режимах:

y = f (z); y =f (u).

Типичный вид такой характеристики показан на рис.1.10.

Рис.1.10. Статическая характеристика САР

Важной величиной, содержащейся в статической характеристике и несущей информацию о точности САР установившихся режимах, является неравномерность регулирования

Δ = y_max - y_min.

Это диапазон изменения регулируемой величины, соответствующий полному диапазону изменения возмущения. Чем меньше эта величина, тем точнее работает САР в статике. Часто используется отношение неравномерности регулирования к среднему значению регулируемой величины

d = D / у _ср ,

которое называется степенью неравномерности и обычно выражается в процентах. В зависимости от конкретной системы степень неравномерности может быть больше или меньше, может быть и равной нулю. В последнем случае система на всех установившихся режимах поддерживает строго одно и то же значение регулируемой величины. Такие САР называют астатическими в отличие от статических, которым свойственно ненулевое (хотя, может быть, и весьма малое) значение степени неравномерности. Несмотря на то, что астатические САР в отношении точности поддержания регулируемой величины в статике превосходят статические, последние широко применяются по причине их простоты и меньшей стоимости.

Динамический режим, иначе называемый переходным процессом, возникает тогда, когда воздействие на систему изменяется во времени. При этом на объекте регулирования возникает небаланс подвода и отвода энергии либо вещества и, как следствие, происходит изменение во времени регулируемой величины. Пример – работа САР частоты тока судовой электростанции при включении дополнительных потребителей электроэнергии.

Динамической характеристикой САР (рис.1.11) называется зависимость регулируемой величины от времени при некоторых заранее оговоренных формах внешних воздействий

y = f (t).

Эта характеристика несёт дополнительную информацию о динамических свойствах системы, которая часто играет определяющую роль. Именно здесь проявляется роль регулятора, тогда как в установившемся режиме, когда нет причины изменения регулируемой величины, достаточно вручную задать объекту регулирования желаемый режим работы.

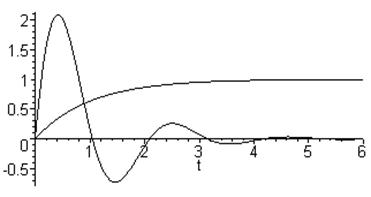
Рис.1.11. Динамические характеристики САР.

1 – статической САР,

2 – астатической САР.

1.10. Типовые внешние воздействия.

Выше упоминалось, что динамическая характеристика соответствует определенным образом оговоренной форме воздействия. Если говорить о реальных воздействиях на систему, то они изменяются случайным образом (рис.1.12).

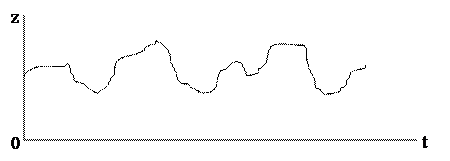Рис.1.12. Реальное воздействие на систему.

Математическое описание воздействий такого характера достаточно сложно, и тем более сложно исследование поведения регулируемой величины при этом. Для упрощения в теории автоматического регулирования принимают некоторые более простые в математическом плане формы воздействий, по анализу реакций САР на которые можно, тем не менее, сделать содержательные выводы о качестве работы системы. Наиболее часто поведение САР исследуется при действии нижеописанных трёх форм воздействий.

1.Скачкообразное, или ступенчатое, воздействие (рис.1.13). Считается, что до некоторого момента времени, условно принимаемого за нулевой, воздействие отсутствовало. В момент t=0 внезапно возникает воздействие, например, возмущение z = z ₀ = const. и остается таким так долго, сколько нас интересует.

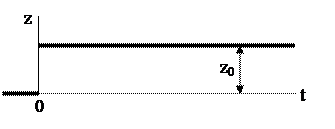
Рис.1.13. Скачкообразное воздействие.

t < 0 ® z = 0;

t ³ 0 ® z = z ₀ = const.

Реально такие воздействия существовать не могут, поскольку не могут существовать мгновенные изменения в каких-либо процессах. Полезность и важность применения такой формы воздействия объясняется тем, что внезапные воздействия для любой системы (включая и человека) являются очень тяжёлыми, и, если система справляется с такими воздействиями, то она тем более работоспособна при воздействиях, более плавно изменяющихся во времени.

Отметим, что при

z ₀ = 1

ступенчатая функция называется функцией Хевисайда, а реакция системы на воздействие типа функции Хевисайда называется переходной функцией системы.

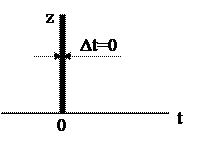2. Импульсное воздействие. Если формально выполнить дифференцирование функции Хевисайда в пределах (-¥ ¼+¥), то получим функцию импульсного воздействия, которая называется функцией Дирака (рис.1.14).

Рис.1.14. Импульсное воздействие.

t ¹ 0 ® z = 0, t = 0 ® z = ¥.

Это воздействие типа удара, также очень тяжелое для системы. Реакция САР на воздействие типа функции Дирака носит название импульсной переходной функции, или функции веса.

3.Периодическое воздействие, повторяющееся с определенным периодом:

y (t +nT _k) = y (t),

где T _k – период колебаний, n – любое целое число.

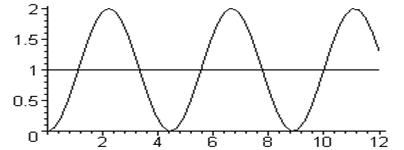
Чаще всего рассматривают колебания гармонического характера (рис1.15):

y = Asin(wt),

где A – амплитуда колебаний,

w - круговая частота колебаний, связанная с периодом колебаний зависимостью

w = 2p / T _k.

t

Рис.1.15. Гармоническое воздействие.

Необходимость изучения поведения системы в условиях действия периодических вынуждающих воздействий диктуется опасностью резонансных явлений. При резонансе амплитуды колебаний регулируемых величин достигают настолько больших значений, что это приводит к аварии объекта регулирования.

2.ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

2.1.Система стабилизации уровня в ёмкости (рис.2.1).

Уровень в цистерне зависит от расходов в единицу времени жидкости на сторонах притока и расхода. При, например, возрастании расхода уровень понижается. Поплавок регулятора (чувствительный элемент) опускается и через рычаг открывает клапан на стороне подвода жидкости (регулирующий орган), увеличивая подвод её. Регулятор прямого действия. Новый установившийся уровень окажется ниже того, который был до увеличения расхода. Это объясняется тем, что так как установившийся режим наступает при равенстве подвода и отвода жидкости, с возрастанием расхода необходимо повысить приток, то есть увеличить открытие клапана, что возможно при условии снижения уровня.

Рис. 2.1. САР уровня жидкости в цистерне.

Регулятор статический, на режимах различных, но постоянных во времени расходов поддерживаемый уровень будет различным.

2.2.Регулятор частоты вращения вала главного судового дизеля (рис.2.2).

При, например, возрастании сопротивления вращению гребного винта частота вращения вала снижается. Грузики регулятора Г (чувствительный элемент) приводятся во вращение от вала двигателя. При снижении частоты вращения центробежная сила грузиков уменьшается, и под действием пружины П (задающее устройство) муфта регулятора М (сравнивающее устройство) перемещается вниз, вызывая через рычаг перемещение рейки топливных насосов Р (регулирующий орган) в сторону увеличения подачи топлива (+).

Рис.2.2. Центробежный регулятор частоты вращения вала прямого действия.

Регулятор прямого действия. Как и предыдущий, он на различных установившихся режимах поддерживает различные частоты вращения, поскольку различным нагрузкам двигателя должны соответствовать различные положения рейки топливных насосов, что по конструкции регулятора возможно при различных положениях муфты, а значит, при различных частотах вращения. Изменением затяжки пружины можно изменить задаваемую частоту вращения.

2.3.Регулятор частоты вращения вала непрямого действия (рис.2.3).

Здесь перемещение муфты приводит к перемещению золотника гидравлического усилителя, открывающего поступление силового масла (от насоса – дополнительного источника энергии) в одну из полостей поршневого сервомотора (исполнительный механизм) и сообщающего другую его полость со сливом. Сервомотор перемещает рейку топливных насосов в направлении соответствующего изменения топливоподачи.

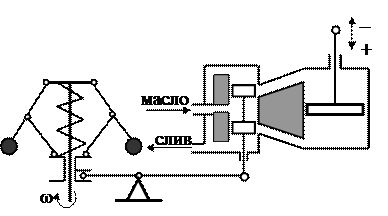
Рис.2.3. Регулятор частоты вращения вала непрямого

действия.

Этот регулятор является астатическим, и объяснить такое его свойство можно путём следующих рассуждений. Установившийся режим наступает, когда прекращается движение рейки топливных насосов. Для этого золотник должен занять единственное положение, соответствующее полному перекрытию масляных каналов его поясками. По конструкции регулятора это возможно при единственном положении муфты, то есть при единственной частоте вращения. Рейка же топливных насосов займёт положение, соответствующее необходимой для конкретного режима топливоподаче.

Из сравнения рассмотренных регуляторов можно сделать заключение: если положение регулирующего органа однозначно связано с положением измерителя, то регулятор и система будут статическими. Если же эта связь не является однозначной, - регулятор и система астатические.

Последнему из рассмотренных регуляторов присущ серьёзный недостаток, заключающийся в возможности колебаний частоты вращения. Дело в том, что в начале переходного процесса происходит быстрое и сильное перемещение золотника и большое открытие им каналов сервомотора. Поршень при этом движется с высокой скоростью и может пройти дальше того положения, которое соответствует новому установившемуся режиму, это вызовет заброс частоты вращения, и регулятору придётся работать в обратном направлении. Достижение нового установившегося режима будет сопровождаться колебаниями регулируемой величины, что часто нежелательно.

С целью уменьшения склонности системы к колебаниям возникает идея: заставить поршень сервомотора замедлять своё движение, организовав воздействие самого поршня на золотник в направлении, противоположном смещению последнего под действием муфты. Это достигается введением в конструкцию регулятора корректирующего устройства - элемента дополнительной обратной связи.

2.4.Регулятор с жёсткой обратной связью (рис.2.4).

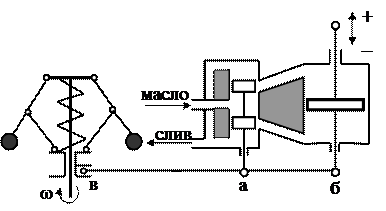Теперь рычаг бав поворачивается вокруг точки в (нынешнего мгновенного центра вращения), и золотник перемещается в направлении закрытия каналов, уменьшая скорость движения поршня и препятствуя тем самым колебаниям рейки топливных насосов. Таким образом, рычаг бав представляет собою корректирующее устройство типа жесткой обратной связи.

Однако получение такого качества работы регулятора достигается ценой снижения точности в установившихся режимах. В самом деле, учитывая условие установившегося режима (единственное положение золотника и точки а) для изменения топливоподачи необходимо изменение положения муфты, а значит, частоты вращения вала.

Стремление улучшить и это качество приводит к идее организации такой обратной связи, которая бы в начале переходного процесса работала аналогично только что рассмотренной, а в конце процесса регулирования исчезала бы. В автоматике такие связи называют гибкими, или исчезающими.

2.5. Регулятор с гибкой обратной связью (рис.2.5).

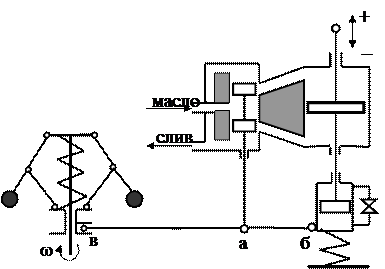Рис.2.5. Регулятор с гибкой обратной связью.

В этой конструкции поршень сервомотора взаимодействует с рычагом обратной связи через цилиндр устройства, именуемого изодромом (в переводе с греческого "изодромный" означает "равнобежный"), представляющим собою комбинацию из пружины и цилиндра с поршнем. Цилиндр заполнен маслом и имеет канал для перетекания масла, снабжённый клапаном, проходное сечение которого можно изменять. Поршень изодрома жестко связан с поршнем сервомотора. Пружина изодрома в установившихся режимах полностью разгружена, поэтому точка б на установившихся режимах находится в единственном положении, в единственном же положении находится и золотник, а потому и муфта регулятора, что соответствует постоянной частоте вращения вала на всех установившихся режимах. Поршень сервомотора и рейка топливоподачи занимают соответствующее нужное положение.

В переходных же процессах, особенно в их начале, при быстром движении поршня сервомотора он увлекает за собой цилиндр изодрома, поскольку масло не успевает перетекать между полостями вследствие малого проходного сечения клапана, и тем самым рычаг бав оказывает на золотник действие, описанное в предыдущем случае.

3. ЛИНЕЙНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ

Линейные системы описываются линейными дифференциальными уравнениями. Математический аппарат линейных систем достаточно хорошо разработан и удобен для исследования, поэтому во многих случаях стремятся, если это принципиально допустимо, использовать именно линейное математическое описание. Несмотря на существование современных компьютерных средств решения задач автоматики, само их применение является эффективным только при условии глубоких знаний теоретической базы. Ниже рассматриваются основные вопросы линейной теории.

3.1.Объект регулирования.

Вывод дифференциального уравнения объекта.

В качестве объекта регулирования рассмотрим главный судовой дизель с прямой передачей мощности на гребной винт регулируемого шага. Регулируемая величина – частота вращения гребного вала, изменение которой может происходить вследствие изменения момента движущих сил М_д, развиваемого двигателем, и момента сил сопротивления М_с со стороны винта. Исходным уравнением, отражающим физические процессы в рассматриваемом объекте, является уравнение неустановившегося вращательного движения

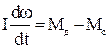, (3.1)

где w - частота вращения вала, I- момент инерции подвижных элементов системы, приведенный к валу, t – время.

Рассмотрим установившийся режим, характеризующийся равенством момента движущих сил и момента сил сопротивления. Здесь и в дальнейшем нулевыми индексами будем сопровождать величины, относящиеся к исходному установившемуся режиму.

М _{д 0} = М _{с 0} ,

следовательно, w₀ = const. На рис.3.1 показаны скоростные характеристики: одна из частичных М _д и одна из винтовых М _с. Точка их пересечения соответствует установившемуся режиму (точка А).

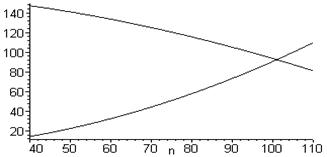
Рис. 3.1. Скоростные характеристики главного

судового двигателя

Перейдём к неустановившемуся режиму. Он возникает при небалансе между подводом и отводом энергии, то есть когда М_д ¹ М_с и, следовательно, частота вращения изменяется во времени: w = var.

Переменные частоту вращения и моменты можно представить в виде сумм их значений на установившемся режиме и приращений:

М _д = М _{д 0} +DМ _д; ; М _с = М _{с 0} + DМ _с; w = w ₀ +Dw.

Момент движущих сил является функцией частоты вращения и положения рейки топливных насосов S, а момент сил сопротивления – функцией частоты вращения, относительной поступи гребного винта l и его шагового отношения h = H/D:

М _д = f (w, S); М _с = f (w, l, h). (3.2)

Точные аналитические выражения для этих функций не существуют. Поэтому стремятся использовать приближённые математические описания. Для подобных целей широко применяется метод малых отклонений, существо которого заключается в следующем.

По самой задаче автоматического регулирования отклонения регулируемой величины от заданного её значения должны быть малы. Поскольку рассматриваемые функции могут быть представлены в виде рядов Тейлора

M_д=M_дo+, (3.3)

можно пренебречь старшими членами рядов, содержащими приращения переменных в степенях выше первой, и тогда мы приходим к линейному математическому описанию:

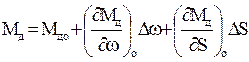, (3.4)

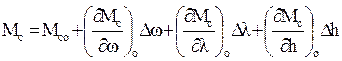. (3.5)

В этих формулах частные производные представляют собою тангенсы углов наклона касательных к соответствующим характеристикам в точке установившегося режима, и они могут быть определены соответствующей обработкой скоростных характеристик конкретного двигателя.

Примем также во внимание, что, поскольку w ₀ = const.,

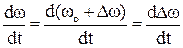(3.6)

Подставим (3.4), (3.5) и (3.6) в уравнение (3.1). После переноса всех членов, содержащих Dw, в левую часть получаемого уравнения оно примет вид

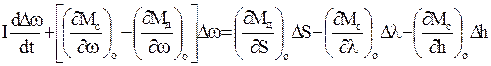. (3.7)

Разделив на выражение в квадратных скобках и приняв обозначения

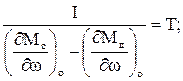
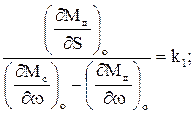
(3.8)

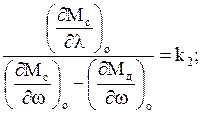
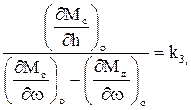
получим дифференциальное уравнение объекта регулирования в приращениях и в размерной форме записи:

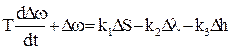. (3.9)

В автоматике часто применяется безразмерная (относительная) форма записи, при которой изменения переменных рассматриваются по отношению к значениям этих переменных на установившемся режиме. Обычно это исходный установившийся режим. Введя обозначения

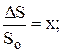
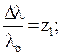
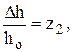(3.10)

где, кроме уже известных величин, S_0,l_0,h₀ – значения положения рейки, относительной поступи и шагового отношения на исходном установившемся режиме, и выполнив нижеприведенные преобразования, получим дифференциальное уравнение объекта регулирования в приращениях и в безразмерной форме записи:

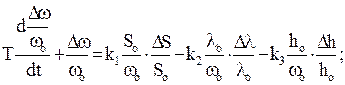
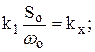
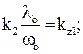
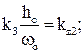
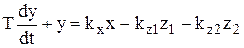. (3.11)

Коэффициенты этого уравнения k_x, k_z1 и k_z2 называются соответственно коэффициентом усиления (иногда коэффициентом передачи) объекта по регулирующему воздействию и коэффициентaми усиления по возмущениям. Это величины безразмерные. Коэффициент Т имеет размерность единиц времени и называется постоянной времени объекта. Для небольших отклонений от установившегося значения частоты вращения (плюс-минус 5%, например) эти коэффициенты можно с достаточной степенью точности считать постоянными. Для режимов же, далеко отстоящих один от другого, их следует определять каждый раз заново. Заметим, что при работе двигателя на винт фиксированного шага возмущение z₂ отсутствует.

Решение уравнения объекта регулирования.

Целью решения является определение закона изменения регулируемой величины y(t) при известных x(t), z₁(t), z₂(t). Физически это эквивалентно нахождению процесса изменения частоты вращения вала во времени, если известны процессы изменения во времени положения рейки топливных насосов, относительной поступи винта и шагового отношения.

Мы имеем дело с линейным неоднородным дифференциальным уравнением первого порядка. Для всех систем, описывающихся линейными дифференциальными уравнениями, справедлив принцип суперпозиции, согласно которому общий эффект от действия на систему суммы нескольких факторов равен сумме эффектов, вызываемых каждым отдельным фактором. Применительно к нашему объекту это означает, что можно рассмотреть изменение регулируемой величины под влиянием каждого из возмущений раздельно, а затем полученные результаты алгебраически сложить. Поэтому будем рассматривать уравнение

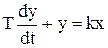, (3.12)

где для простоты индекс при коэффициенте опущен.

Решение этого уравнения ищется в виде

,

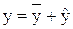где 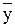- общее решение соответствующего однородного уравнения

,

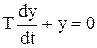- частное решение уравнения (3.12).

В качестве частного решения обычно интересуются новым установившимся значением регулируемой величины, то есть тем, которое она примет по окончании переходного процесса, вызванного воздействием в данном случае x. Примем, что закон изменения x – скачкообразный:

t < 0, x = 0, t ³ 0, x = x ₀ =const.

В нашем случае это соответствует мгновенному изменению относительного положения рейки топливоподачи на величину x₀. Таким образом, условия нового установившегося режима выглядят так:

x = x₀; 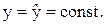(3.13)

Подставив эти условия в уравнение (3.12), получим

y = kx ₀.

Общее решение однородного уравнения ищется в форме

,

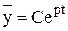где C – постоянная интегрирования, p – корень характеристического уравнения

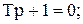
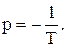
Таким образом,

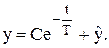(3.14)

Постоянная интегрирования определяется на основании начальных условий. Обычно в качестве таковых задаются условиями исходного установившегося режима, когда ещё не было изменения регулируемой величины, и они выглядят так:

t = 0, y=0.

Подставив начальные условия в уравнение (3.14), получим

,

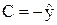и окончательно

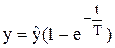. (3.15)

График переходного процесса.

На рис.3.2 представлен график переходного процесса. Здесь ЛНУР – линия нового установившегося режима. Очевидно, что она является асимптотой для кривой - графика переходного процесса. Эта кривая (в математике она имеет специальное название – экспонента) обладает следующим свойством: отрезок, отсекаемый на ЛНУР касательной к экспоненте в какой-либо точке и перпендикуляром из этой точки, численно равен постоянной времени. Тогда можно дать толкование физическому смыслу постоянной времени, если рассмотреть такое построение из начала координат.

Постоянная времени – это время, за которое регулируемая величина достигла бы значения, соответствующего новому установившемуся режиму, если бы она изменялась с постоянной скоростью, равной начальной скорости её изменения.

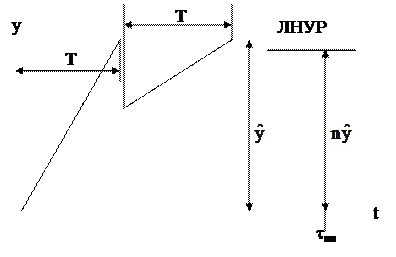
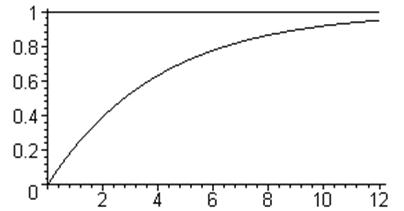
Рис.3.2. График переходного процесса в объекте регулирования

и постоянная времени.

Продолжительность переходного процесса

в объекте регулирования.

Теоретически для любого объекта выход регулируемой величины на новое установившееся значение продолжается бесконечно долго. На практике же можно встретить объекты, в которых переходный процесс происходит быстрее или медленнее. В автоматике широко применяется инженерное понятие продолжительности переходного процесса. Это такое время t_пп, за которое регулируемая величина становится достаточно близкой к своему установившемуся значению (рис.3.2):

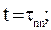
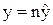. (3.16)

Здесь величина n близка к единице и характеризует точность приближения к установившемуся режиму.

Подставив (3.16) в (3.15) и выполнив упрощение, получим

.

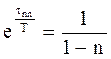После логарифмирования обнаруживается связь между временем переходного процесса и постоянной времени:

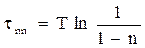. (3.17)

Часто считают переходный процесс практически окончившимся, когда регулируемая величина достигает 95% от нового установившегося значения, то есть принимают n = 0, 95. При этом оказывается, что

t_пп @ 3Т.

Приведём практически встречающиеся значения постоянных времени судовых объектов регулирования, которые в первом приближении могут быть описаны уравнением типа (3.9).

Судовые главные дизели – около 1 секунды.

Газотурбонагнетатели – несколько секунд.

Дизельгенераторы – 3…4 секунды.

Судовые паровые котлы – 10…15 минут.

Судно относительно изменения его скорости – 1…5 минут.

Различные теплообменные аппараты – минуты.

Электродвигатели – около 1 секунды.

3.2. Типовые динамические звенья.

Выше мы познакомились с примером математического описания одного из элементов САР. В системах автоматики существуют звенья, имеющие и другое описание. Отметим прежде всего, что имеются в виду элементарные звенья. Звено называют элементарным, если оно не может быть представлено как комбинация двух или более звеньев. Независимо от физической природы протекающих процессов всё многообразие элементарных звеньев по математическому описанию сводится к шести типам. Ниже они будут рассмотрены, и показаны графики переходных процессов в этих звеньях при скачкообразном сигнале на входе.

1.Безинерционное звено:

y = kx.

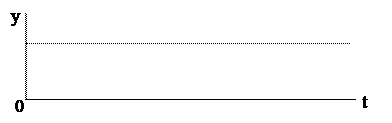Свойства этого звена таковы, что оно мгновенно, без какого-либо запаздывания передаёт входной сигнал на выход (рис.3.3).Иногда поэтому его называют идеальным по быстродействию.

Рис.3.3. Безинерционное звено.

Поскольку любое из реально существующих звеньев обладает большей или меньшей инерционностью, такое представление о динамических свойствах звена является определенной идеализацией, допустимой лишь при сравнении двух инерционных звеньев по продолжительности переходных процессов в них. По современному состоянию техники одно звено можно считать безинерционным по сравнению с другим, если постоянная времени первого хотя бы в 50 раз меньше, чем постоянная времени второго. Так, часто в процессах вывода на заданный режим главный судовой двигатель можно считать безинерционным по сравнению с судном.

2.Апериодическое звено первого порядка. К этому типу звеньев относится рассмотренный ранее объект регулирования (рис. 3.4).

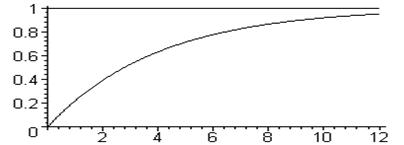
Рис. 3.4. Апериодическое звено 1 порядка.

3.Интегрирующее звено:

.

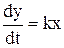Прямое интегрирование при нулевых начальных условиях дает

.

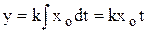График переходного процесса приведен на рис. 3.5. Примерами таких звеньев являются различные счётчики, многие исполнительные механизмы.

Рис.3.5. Интегрирующее звено.

4.Дифференцируюшее звено:

.

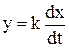Это тоже в некотором роде идеализация. При скачкообразном сигнале на входе в моменты времени, не равные нулю, сигнал на выходе равен нулю, а в нулевой момент времени выходной сигнал имеет вид импульса, бесконечно большого по величине и бесконечно малого по продолжительности (рис.3.6)

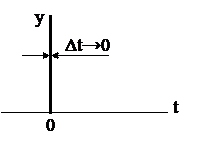Рис. 3.6. Идеальное дифференцирующее звено.

5.Звено с «чистым», или транспортным запаздыванием. В таком звене выходная величина повторяет входную с отставанием на время «чистого» запаздывания t₃ (рис. 3.7):

y(t+t₃) = x(t).

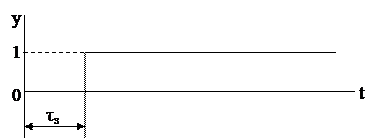Рис. 3.7. Звено с «чистым» запаздыванием.

6. Звено второго порядка. Познакомимся с выводом и решением дифференциального уравнения такого звена на примере центробежного регулятора частоты вращения вала двигателя (рис. 3.8).Входной величиной для регулятора является частота вращения вала, выходной – перемещение рейки топливных насосов. Обозначения этих величин такие же, как для объекта регулирования.

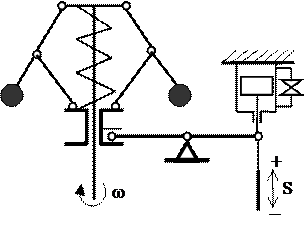Рис. 3.8. Центробежный регулятор.

В схему этого регулятора введён демпфер, дающий возможность гасить колебания рейки топливоподачи и конструктивно похожий на цилиндр изодрома регулятора непрямого действия с гибкой обратной связью (рис. 2.5). Примем для простоты, что рычаг равноплечий и потому перемещения муфты и рейки одинаковы и равны S.

Муфта находится под действием следующих сил.

- F_ц – приведенная к муфте центробежная сила грузов:

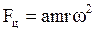. (3.18)

Здесь m – суммарная масса грузов;

r – расстояние грузов от оси вращения;

a – коэффициент, учитывающий кинематику передачи от грузов к муфте.

- F_п – сила со стороны пружины, равная

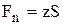, (3.19)

где z – жесткость пружины.

- F_д – сила со стороны демпфера, пропорциональная скорости движения муфты:

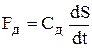, (3.20)

где С_д – коэффициент сопротивления демпфера.

- F_и – сила инерции:

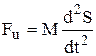, (3.21)

где М – приведенная к муфте масса подвижных частей регулятора.

- G – сила тяжести, приведенная к муфте.

Применяя принцип Даламбера и учитывая направления действия сил, можно записать уравнение динамики движения муфты в виде

F_и + F_д + F_п + G = F_ц.

Переходя к приращениям, получаем

DF_и + DF_д + DF_п = DF_ц. (3.22)

Слагаемые левой части этого уравнения линейно зависят от S, а правая часть применением метода малых отклонений приобретает вид:

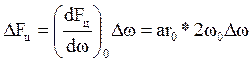. (3.23)

Таким образом, в малых отклонениях движение рейки описывается уравнением

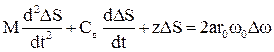. (3.24)

Разделив на z и приняв обозначения

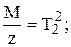
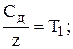
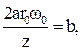(3.25)

получим дифференциальное уравнение регулятора в приращениях и в размерной форме записи:

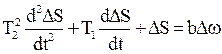. (3.26)

В безразмерной форме уравнение имеет вид

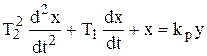. (3.27)

Здесь принято обозначение

.

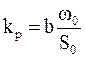Коэффициент k_p называется коэффициентом усиления регулятора, а коэффициенты Т₂² и Т₁ имеют размерности соответственно квадрата и первой степени времени. Такое обозначение логично и удобно.

Решение уравнения звена второго порядка.

В результате решения мы получим закон изменения во времени выходной величины регулятора x. Примем, как это уже стало привычным, что входная величина изменяется скачкообразно:

t < 0, y = 0; t ³ 0, y = y₀ = const.

Решение уравнения (3.27) ищется в форме

x = +,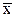

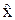где 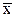- общее решение соответствующего однородного уравнения

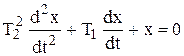, (3.28)

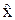- частное решение уравнения (3.27).

По аналогии со случаем, рассмотренным в разделе “объект регулирования”, частное решение как новое установившееся значение выходной величины будет

.

Общее решение уравнения (28) ищется в форме

,

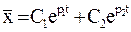
где C₁ и C₂ – постоянные интегрирования, p₁ и p₂ – корни характеристического уравнения

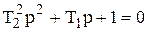. (3.29)

Таким образом,

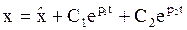. (3.30)

Постоянные интегрирования, как и в случае объекта регулирования, определим на основании начальных условий. Исходный установившийся режим характеризуется следующими условиями:

t=0; x=0; 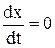. (3.31)

Подстановка (3.31) в (3.30) даёт

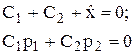. (3.32)

Отсюда постоянные интегрирования

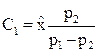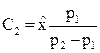; , (3.33)

и окончательно

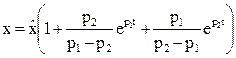. (3.34)

В зависимости от вида корней характеристического уравнения (вещественные, комплексные либо чисто мнимые) имеется три частных случая. Обратим, однако, внимание на то, что решение уравнения (3.27) в форме (3.34) получено для общего случая, независимо от вида корней.

6.А.В случае, когда выполняется условие

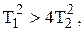
характеристическое уравнение имеет два вещественных отрицательных корня

,

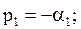
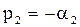и переходный процесс описывается формулой

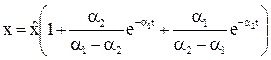. (3.35)

Соответствующий график переходного процесса показан на рис.3.9. Звено в этом случае называется апериодическим звеном второго порядка, чем подчёркивается факт отсутствия колебаний в переходном процессе.

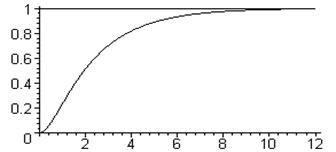
Рис. 3.9. Переходный процесс апериодического звена 2 порядка

6.Б. В случае, когда

,

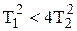корни характеристического уравнения комлексно-сопряжённые с отрицательной вещественной частью:

.

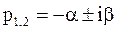Подстановка этих значений в выражение (34) с учётом того, что, согласно формуле Эйлера,

e ^±ibt =cosbt ± isinbt,

после простых преобразований приводит к такому результату:

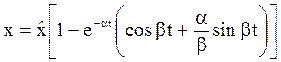. (3.36)

График переходного процесса для этого случая показан на рис. 3.10. Звено называется колебательным, и период колебаний выражается через частоту свободных колебаний так:

T_кол=2p/b. (3.37)

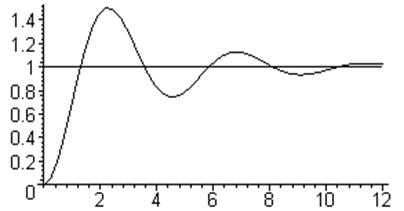
Рис. 3.10. Переходный процесс колебательного звена