Отношение Ау/Ах есть модуль АФХ и является функцией частоты:
Ау/Ах=R(w)
и называется амплитудно- частотной характеристикой (АЧХ). Фазовый
сдвиг j =j (w) - также функция частоты и называется фазовой частотной характеристикой (ФЧХ). Вычисляя R(w) и j(w) для диапазона частот (0…¥), можно построить на комплексной плоскости в координатах M(w) и iN(w) график АФХ (рис.3.17).
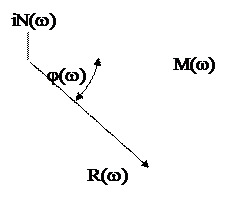
Рис.3.17. График АФХ.
Очевидны следующие соотношения:
M = Rcosj; N = Rsinj;
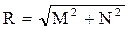 ; j = arctg(N/M). (3.61)
; j = arctg(N/M). (3.61)
Амплитудно-частотная характеристика.
АЧХ любой системы представляет наибольший интерес, поскольку даёт возможность определить амплитуду колебаний выходной величины при известных амплитуде и частоте входной величины. На рис. 3.18 показаны возможные на практике виды АЧХ.
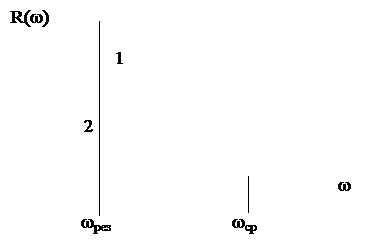 |
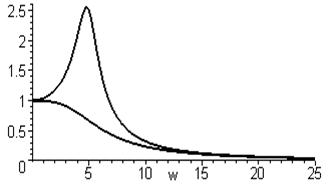
Рис.3.18. Амплитудно-частотные характеристики.
На АЧХ системы 1 виден резонансный пик, соответствующий наибольшей амплитуде вынужденных колебаний. Работа в зоне около резонансной частоты может оказаться губительной и часто вообще недопустима правилами эксплуатации конкретного объекта регулирования. АЧХ вида 2 не имеет резонансного пика и для механических систем более предпочтительна. Видно также, что с увеличением частоты амплитуда выходных колебаний уменьшается. Физически это легко объясняется: любая система в силу присущих ей инерционных свойств легче подчиняется раскачиванию низкими частотами, чем высокими. Начиная с некоторой частоты, колебания на выходе становятся незначительными, и эту частоту называют частотой среза, а диапазон частот ниже частоты среза называют полосой пропускания частот. В теории автоматического регулирования за частоту среза принимают такую, при которой значение АЧХ в 10 раз меньше, чем при нулевой частоте. Свойство системы гасить высокочастотные колебания называется свойством фильтра низких частот.
Рассмотрим методику расчета АЧХ на примере звена второго порядка, дифференциальное уравнение которого
(T22p2 + T1p + 1)y = kx. (3.62)
В задачах вынужденных колебаний часто используют более наглядную форму уравнения
(p2 +2xw0p + w02)y = kw02x, (3.63)
где 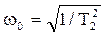 называется собственной частотой колебаний при отсутствии затухания, x =T1w0/2 - коэффициент затухания.
называется собственной частотой колебаний при отсутствии затухания, x =T1w0/2 - коэффициент затухания.
Передаточная функция при этом выглядит так:
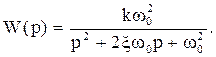
 (3.64)
(3.64)
Заменой p = iw получаем амплитудно-фазовую характеристику
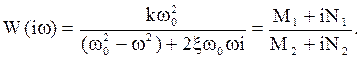 (3.65)
(3.65)
Используя правило деления комплексных чисел, получаем выражение для АЧХ:
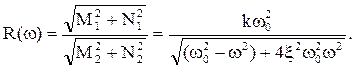 (3.66)
(3.66)
Определим резонансную частоту, при которой АЧХ имеет максимум. Это соответствует минимуму знаменателя выражения (3.66). Приравнивая нулю производную знаменателя по частоте w, имеем:
2(w02 - w2)(-2w) +4x2w02*2w = 0, (3.67)
откуда получаем значение резонансной частоты, не равное нулю:
 wрез = w0Ö 1 - 2x2. (3.68)
wрез = w0Ö 1 - 2x2. (3.68)
Проанализируем это выражение, для чего рассмотрим отдельные случаи, которым соответствуют различные значения коэффициента затухания.
1. x = 0. Резонансная частота равна собственной, и модуль АЧХ при этом обращается в бесконечность. Это случай так называемого математического резонанса.
2. 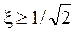 . Поскольку частота выражается положительным числом, а из (68) для этого случая получается либо нуль, либо мнимое число, следует вывод, что при таких значениях коэффициента затухания АЧХ не имеет резонансного пика (кривая 2 на рис.3.18).
. Поскольку частота выражается положительным числом, а из (68) для этого случая получается либо нуль, либо мнимое число, следует вывод, что при таких значениях коэффициента затухания АЧХ не имеет резонансного пика (кривая 2 на рис.3.18).
3.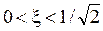 . АЧХ имеет резонансный пик, причём с уменьшением коэффициента затухания резонансная частота приближается к собственной и резонансный пик становится выше и острее.
. АЧХ имеет резонансный пик, причём с уменьшением коэффициента затухания резонансная частота приближается к собственной и резонансный пик становится выше и острее.
3.5. Устойчивость автоматических систем.
Подобно тому, как употребляется термин «устойчивость» в общераспространенном понимании, в автоматике под этим термином тоже в некоторой степени подразумевается способность какой-либо системы противостоять факторам, выводящим систему из равновесия. Строгая формулировка такова.
Устойчивость – это способность системы приходить к состоянию равновесия после прекращения действия факторов, которые вывели её из равновесия. Состояние равновесия характеризуется неизменностью во времени регулируемых величин. Если система не приходит к состоянию равновесия, а бесконечно от него удаляется, она не устойчива. Неустойчивые системы не могут эксплуатироваться, поскольку в них происходит неконтролируемое изменение регулируемых величин. Как правило, потеря системой устойчивости приводит к авариям объекта регулирования, причем часто катастрофического характера. Как примеры можно указать на опрокидывание потерявших остойчивость судов, разрушение двигателей («разнос»), взрывы на предприятиях химического производства и т. д. Таким образом, требование устойчивости является обязательным для любой работоспособной системы. Следует отметить, что потеря устойчивости САР может произойти вследствие изменения её свойств, вызванного как износом или отказом элементов, так и (весьма нередко) неквалифицированными действиями человека при попытке изменить настройку системы либо в процессе выполнения профилактических мероприятий. Заметим также, что понятие устойчивости имеет качественный характер, но не количественный. Так, о системе можно сказать, что она устойчива либо неустойчива, но нельзя говорить, что система «более» либо «менее» устойчива.
Характер переходных процессов в устойчивых и неустойчивых системах при действии внешних факторов можно видеть на рис.3.19. Устойчивые системы по окончании переходного процесса приходят к некоторому установившемуся значению регулируемой величины (рис.3.19,а), в неустойчивых системах (рис.3.19,б) регулируемая величина неограниченно изменяется. Если же процесс в системе носит характер установившихся колебаний (как граничный между затухающими и расходящимися колебаниями), то говорят, что система находится на границе устойчивости (рис.3.19,в). Понятно, что только вариант (3.19,а) приемлем для практического применения. Таким образом, внешним признаком устойчивой системы является ограниченность регулируемой величины: у = огр.

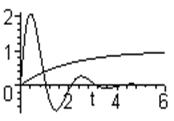
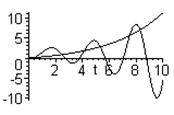
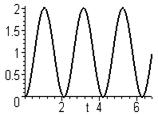
Рис.3.19. Переходные процессы в системах:
а – устойчивых; б – неустойчивых;
в – САР на границе устойчивости.
Исходными данными для решения задачи об устойчивости системы является её математическое описание. Первое решение такой задачи, не лишенное недостатков, дал английский физик Джеймс Максвелл (1868).
Оценка устойчивости САР по корням её
характеристического уравнения (теорема Максвелла)
Пусть система описывается дифференциальным уравнением
(anpn + an-1pn-1 + …+ a1p + a0) y = bx. (3.69)
Решение его, как любого линейного уравнения, ищется в виде
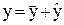 ,
,
где 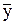 - общее решение однородного уравнения
- общее решение однородного уравнения
(anpn + an-1pn-1 + …+ a1p + a0) y=0, (3.70)
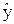 - частное решение уравнения (3.69).Условием ограниченности у является ограниченность этих обоих слагаемых.
- частное решение уравнения (3.69).Условием ограниченности у является ограниченность этих обоих слагаемых.
Как всегда, частное решение – это значение регулируемой величины на новом установившемся режиме, вызванном воздействием х=х0:
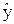 = const.; x = x0.
= const.; x = x0.
Подстановка в (3.69) даёт условие установившегося режима:
а0 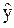 = bx0,
= bx0, 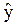 =bх0 /а0.
=bх0 /а0.
В реальных условиях воздействие всегда ограничено по величине, и поэтому частное решение ограничено. Отсюда следует важный вывод: правая часть дифференциального уравнения не влияет на устойчивость линейной системы, следовательно, от внешних воздействий не зависит, обладает система свойством устойчивости или нет. Таким образом, устойчивость САР определяется только видом левой части её уравнения. Общее решение:
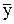 = C1exp(p1t)+ C2exp(p2t)+…+ Cnexp(pnt), (3.71)
= C1exp(p1t)+ C2exp(p2t)+…+ Cnexp(pnt), (3.71)
где С1, С2, … Сn – постоянные интегрирования, p1, p2 , … pn – корни характеристического уравнения
anpn + an-1pn-1 + …+ a1p + a0 = 0.
Поскольку постоянные интегрирования есть ограниченные величины, очевидно, что ограниченность общего решения зависит от вида функций
exp(pkt), k = 1,2,… n,
то есть от корней характеристического уравнения. В общем случае среди корней могут быть вещественные, комплексные и мнимые. Каждому виду корней в выражении (71) соответствует определенный вид слагаемого и, естественно, требуется ограниченность каждого из них (табл.1).
Табл.1
| Вид корня | Вид слагаемого | |
| вещественный pk = ak | Ckexp(akt) | |
| комплексные pk,k+1=ak±wki | exp(akt)[Ckcos(wkt)+Ck+1sin(wkt)] | |
| Mнимые pk,k+1=±wki | Ckcos(wkt)+Ck+1sin(wkt) |
Третий случай даёт незатухающую составляющую в общем решении, и если остальные составляющие являются сходящимися, то система находится на границе устойчивости. Это свойство часто используется при анализе устойчивости САР. Выражение в квадратных скобках есть ограниченная величина. Таким образом, ограниченность общего решения зависит от того, ограничены или нет функции exp(akt) для всех k Î[1,n]. При очевидном t > 0 для этого требуется, чтобы
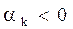
, k = 1,2,… n. (3.72)
Теорема Максвелла: для устойчивости линейной системы необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения этой системы были отрицательны.
Частные случаи: достаточные условия устойчивости систем первого и второго порядков.
Характеристическое уравнение САР 1 порядка
а1р +а0 =0
имеет единственный вещественный корень р = -а0/а1.Он отрицателен, если оба коэффициента имеют одинаковые знаки. Имея в виду возможность изменения знаков обоих коэффициентов на обратные, достаточное условие устойчивости можно сформулировать как требование положительности коэффициентов характеристического уравнения.
Характеристическое уравнение САР 2 порядка
а2р2 + а1р +а0 = 0
имеет корни
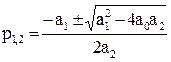 .
.
Анализ этого выражения приводит к заключению, что и здесь достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения, а если коэффициенты отличаются по знаку, то система неустойчива.
Устойчивость САР высоких порядков.
Для устойчивости систем 3 и более высоких порядков требование положительности всех коэффициентов характеристического уравнения является необходимым, но не достаточным. Другими словами, если все корни имеют отрицательные вещественные части, то все коэффициенты будут положительны, но обратное утверждение не справедливо.
Вычисление корней уравнений третьей и четвертой степеней связано со значительными трудностями, а корни уравнений пятой и более высоких степеней согласно теореме Абеля не могут быть выражены через коэффициенты с использованием знаков алгебраических действий и операции извлечения квадратного корня. Это значит, что при несомненной справедливости теоремы Максвелла её использование ограничено. Поэтому разработаны такие способы анализа устойчивости систем, когда не требуется нахождение корней. Все эти способы получили название критериев устойчивости. Здесь мы считаем возможным рассмотреть наиболее употребительные из них.
Критерий Гурвица (1895).
Уравнение системы порядка n
anpn + an-1pn-1 + an-2pn-2+ … +a2p + a1p + a0 = 0
будет иметь корни с только отрицательными вещественными частями при выполнении следующих требований:
все коэффициенты характеристического уравнения и все диагональные миноры определителя Гурвица должны быть положительны:
аk > 0, k = 0,1,2,…,n; Mk > 0, k = 0,1,2,…,n-1.
Правило составления определителя Гурвица.
 |
an-1 an-3 an-5 ………………... 0
an an-2 an-4 …………………..
0 an-1 an-3.…………………..
0 an an-2 …………………...
M0 = ……. … ………………………………….
. 0 …………………….a0…..0
. 0 ….…………………a1 0
0 0 …..…………………a2 a0
По главной диагонали располагаются последовательно коэффициенты уравнения, начиная со второго слева. Расположение коэффициентов в колонках в направлении сверху вниз соответствует их расположению в уравнении в направлении справа налево. Места отсутствующих коэффициентов заполняются нулями. Диагональные миноры – это определители, получающиеся из определителя Гурвица последовательным вычеркиванием правых колонок и нижних строк. Например, минор с индексом (n-3) выглядит так:

 an-1 an-3 an-5
an-1 an-3 an-5
M n-3 = an an-2 an-4 = an-1an-2an-3 + anan-1an-5 – anan-32 – an-4an-12
0 an-1 an-3.
Заметим, что в принятом нами порядке индексации индекс минора совпадает с индексом коэффициента, стоящего в его нижнем правом углу.
Модификация критерия Гурвица – критерий Льенара-Шипара. Авторы этого критерия установили, что можно обойтись меньшим количеством неравенств, чем это требуется по критерию Гурвица. Согласно этому критерию, требование положительности всех диагональных миноров заменяется требованием положительности диагональных миноров с нечетными индексами.
Критерий Михайлова (1938).
Пусть собственный оператор системы имеет вид
D(p) = anpn + an-1pn-1 + … + a1p + a0. (3.73)
Если р1, р2 ,…, рn – его корни (пусть неизвестные нам), то он, согласно теореме Безу, может быть представлен в виде произведения
D(p) = an(p – p1)(p – p2)…(p – pn). (3.74)
Произведём замену p = iw:
D(iw) = an(iw - p1)(iw - p2)…(iw - pn) = U(w) + iV(w). (3.75)
Исследуем на комплексной плоскости в координатах (a, iw) поведение вектора (iw - pk) при изменении w от -¥ до +¥, причём a и w - вещественная и мнимая части корня pk. Поскольку для устойчивой системы a < 0, построения располагаются слева от мнимой оси (рис.3.20).
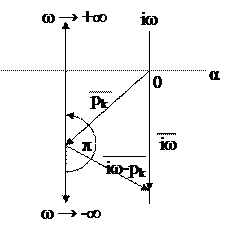 |
Рис.3.20. Поведение вектора-разности.
При изменении w от -¥ до +¥ вектор-разность поворачивается в положительном направлении на угол p:
arg (iw - pk) = p, wÎ(-¥,+¥).
Вектор D(iw) = U(w) + iV(w) есть произведение векторов, и при изменении w от -¥ до +¥ его поворот составит np, как сумму поворотов отдельных векторов:
arg [U(w) + iV(w)] = np, wÎ(-¥,+¥).
Давая w значения в диапазоне (-¥,+¥) и вычисляя компоненты вектора U(w) и V(w), на комплексной плоскости можно построить кривую в координатах U и iV. Эта кривая симметрична относительно вещественной оси. Обычно рассматривают её половину, соответствующую изменению w в диапазоне (0,+¥), и эта кривая называется кривой Михайлова. Очевидно, что для этого диапазона изменения w поворот вектора U(w) + iV(w) составит
arg [U(w) + iV(w)] = n(p/2), wÎ(0,+¥).
Отсюда следует формулировка критерия Михайлова.
САР устойчива, если кривая Михайлова начинается на положительной части вещественной оси и проходит последовательно столько четвертей комплексной плоскости, каков порядок уравнения системы.
Примеры кривых Михайлова для устойчивых систем различных порядков приведены на рис.3.21.
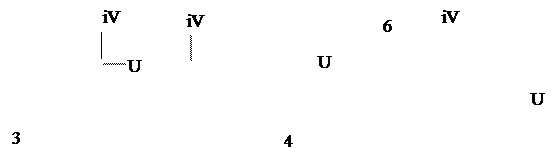
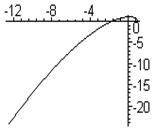
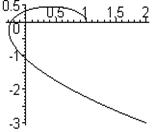
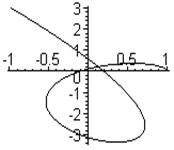
Рис.3.21. Кривые Михайлова устойчивых САР 3, 4, и 6 порядков.
Для неустойчивых САР кривые Михайлова не проходят последовательно должное количество четвертей (рис.3.22).

Рис.3.22. Неустойчивая САР 4 порядка.
Применение критерия Михайлова.
1. Записывается собственный оператор системы
D(p) = anpn + an-1pn-1 + … + a1p + a0.
2. Производится подстановка р = iw:
D(iw) = an(iw)n + an-1(iw)n-1 + … +a2(iw)2 +a1iw +a0 = U(w) + iV(w).
3. Выделяются вещественная и мнимая части:
U(w) = a0 - a2 w2 + a4 w4 – a6w6 +…;
V(w) = a1w – a3 w3 + a5w5 -a7 w7 +…
4. Приняв для w ряд значений в диапазоне (0, ¥), рассчитываются соответствующие значения координат вектора кривой Михайлова и строится эта кривая.
5. По виду кривой делается заключение об устойчивости.
Примечание. Для любой системы кривая Михайлова уходит в бесконечность в той четверти, каков порядок системы, и это свойство следует использовать при выборе диапазона изменения w.
Критерий Найквиста (1932).
Этот критерий позволяет судить об устойчивости замкнутой САР по виду амплитудно-фазовой характеристики этой системы в разомкнутом состоянии. Между АФХ разомкнутой системы Wp и замкнутой W3 соотношения таковы:
W3 = Wp/(1+Wp); Wp = W3/(1- W3).
Рассмотрим схему САР на рис.3.23. Система, имеющая передаточную функцию в разомкнутом состоянии Wp, замкнута единичной отрицательной главной обратной связью.
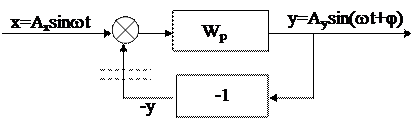 |
Рис.3.23. Замыкание разомкнутой САР.
Мысленно разорвём замкнутую цепь в месте, указанном пунктиром. Возбудим на входе гармонические колебания х. На выходе разомкнутой системы возникнут колебания
y = Aysin(wt+j),
а на выходе звена обратной связи колебания будут иметь обратный знак, что можно трактовать как смещение по фазе на угол p:
y = - Aysin(wt+j) = Aysin(wt+j - p).
Примем некоторую частоту, при которой фазовый сдвиг, получающийся в разомкнутой системе,
j = p.
Если при этой частоте амплитуда Ау окажется меньше, чем Ах, то это означает, что при прохождении через разомкнутую САР колебания затухают, и САР в замкнутом состоянии будет устойчива. Если наоборот – замкнутая САР неустойчива. Поскольку отношение амплитуды выходных колебаний к амплитуде входных есть модуль АФХ, он при частоте, соответствующей фазовому сдвигу p, для устойчивой системы меньше единицы. Отсюда следует формулировка критерия Найквиста.
Замкнутая система будет устойчивой, если соответствующая разомкнутая система устойчива, и АФХ последней не охватывает точку с координатами (-1,0i) (рис.3.24).
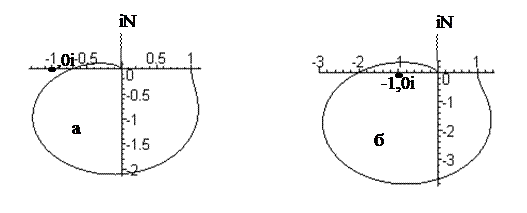 |
Рис.3.24. АФХ разомкнутых систем:
а - замкнутая система устойчива;
б – замкнутая система неустойчива.
D- разбиение пространства параметров.
Этот способ анализа САР на устойчивость отличается от других тем, что даёт ответ не только на вопрос, устойчива САР или нет, но и позволяет определить для некоторых интересующих нас параметров системы области этих параметров, в которых САР сохраняет свойство устойчивости. Наиболее распространено D- разбиение по двум параметрам.
Пусть характеристическое уравнение САР имеет вид
anpn+an-1pn-1+…+Apk +…+ Bps +…+a1p+a0=0, (3.76)
где A и B- коэффициенты уравнения, для которых мы хотим найти те области, где САР устойчива. Выведем систему на границу устойчивости, для чего потребуем наличия чисто мнимых корней уравнения (3.76) p = iw:
an(iw)n+an-1(iw)n-1+…+A(iw)k+…+B(iw)s+…+a1(iw)+a0=0. (3.77)
Записанное слева комплексное число равно нулю по определению тогда, когда равны нулю его вещественная и мнимая части. Выделив их, получим:
F1(A,w) = 0; F2(B,w) = 0. (3.78)
Иногда удаётся из этих уравнений исключить w, и тогда получают зависимость
B = f(A). (3.79)
Функция B = f(A) является границей устойчивости и отображает мнимую ось комплексной плоскости корней. Она делит область возможных по необходимому условию устойчивости значений А и В на области устойчивости и неустойчивости. Для выделения области устойчивости проще всего поступить так. Задаться в какой-нибудь области точкой с координатами (А=А1, В=В1) и с помощью какого-либо из рассмотренных ранее критериев проанализировать эту конкретную систему на устойчивость. Если результат окажется положительным, это означает, что вся область, к которой принадлежит выбранная точка, является областью устойчивости, и её штрихуют по границе с направлением штриховки внутрь. Если линия границы устойчивости имеет самопересечения, то по выходу из заштрихованной области штриховку продолжают с той же стороны по ходу по кривой. Типичным примером D- разбиения является рассматриваемый ниже критерий Вышнеградского.
Критерий Вышнеградского(1876).
Он распространяется на системы третьего порядка и в своё время был разработан в связи с необходимостью анализа САР частоты вращения вала паровой машины с центробежным регулятором прямого действия. Характеристическое уравнение системы
а3р3 + а2р2 + а1р + а0 = 0.
Выполнив замену переменной
p3(a3/a0) = U3,
приходим к выражению
U3 + AU2 + BU + 1 = 0, (3.80)
называемому уравнением Вышнеградского, где коэффициенты
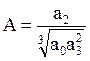 ;
; 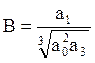
называются параметрами Вышнеградского.
Отметим прежде всего, что необходимые условия устойчивости выражаются в таком виде:
А > 0, В > 0. (3.81)
Выведем систему на границу устойчивости, для чего в уравнение (3.80) подставим р = iw:
(iw)3 + A (iw)2 + B iw + 1 = 0,
что после разделения вещественной и мнимой частей даёт
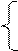 |
1 - Аw2 = 0
Вw - w3 = 0. (3.82)
Из второго уравнения системы (82) подставим в первое w2 = В, тем самым совместно с (81) получим условия границы устойчивости:
А > 0, В > 0, АВ = 1. (3.83)
На диаграмме Вышнеградского (рис.3.25) кривая, называемая гиперболой Вышнеградского, является границей устойчивости, и она делит область возможных значений коэффициентов А и В на две части, одна из которых является областью устойчивости. Для обнаружения этой области рассмотрим заведомо устойчивую систему, корни характеристического уравнения которой
U1 = U2 = U3 = - 1.
Тогда характеристический полином можно представить в виде
U3+AU2+BU+1=(U–U1)(U–U2)(U–U3) =(U + 1)3 =U3+3U2+3U+1,
откуда А = 3, В = 3. Этими координатами определяется точка М на диаграмме, следовательно, область выше гиперболы Вышнеградского есть область устойчивости. Тогда условия устойчивости записываются так:
А > 0, В > 0, АВ > 1.

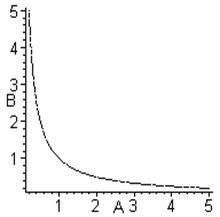
Рис. 3.25. Диаграмма Вышнеградского.
3.6. Качество процессов регулирования.
Под этим термином понимается точность работы САР. В идеальной системе отклонение регулируемой величины от заданного значения вообще отсутствует. В реальной системе оно есть, и о точности системы судят по тому, насколько переходный процесс в реальной системе близок к идеальному. Для численной характеристики точности САР применяют ряд величин, именуемых показателями качества регулирования. Обычно их рассматривают отдельно для неколебательных и для колебательных cистем.
Неколебательные системы (рис.3.26).
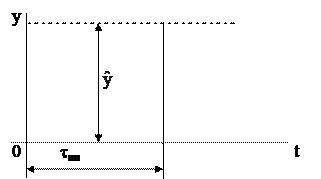 |
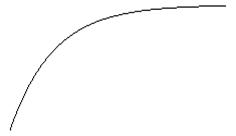
Рис.3.26. Показатели качества регулирования неколебательных систем.
Для них используют только 2 показателя:
1. 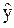 - установившаяся, или статическая ошибка регулирования;
- установившаяся, или статическая ошибка регулирования;
2. tпп – продолжительность переходного процесса.
Колебательные системы (рис.3.27).
Для них, помимо несомненно важных первых двух, применяют ещё такие:
3. D – динамический заброс, то есть наибольшее отклонение регулируемой величины в переходном процессе;
4. tнар – время нарастания, то есть время первого выхода на значение, соответствующее новому установившемуся режиму;
5. К = tпп/Ткол - колебательность, то есть количество колебаний за время переходного процесса.
 |
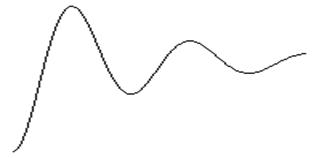
Рис.3.27. Показатели качества регулирования колебательных
систем.
Чем меньше любой из показателей качества, тем лучше система.
Интегральные критерии качества регулирования.
Рассмотренные показатели качества взаимно противоречивы. Так, улучшение путём настройки САР одного из показателей приводит к ухудшению других. Кроме того, часто приходится сравнивать по качеству регулирования системы (даже одного назначения), у которых различные показатели качества отличаются в разные стороны. Очевидно, возникает необходимость производить сравнение по некоторому комплексному показателю, который учитывал бы все отдельные показатели. Такие комплексные показатели называются интегральными критериями качества регулирования (ИККР). ИККР должны удовлетворять следующим требованиям.
1.Критерий должен быть вычислимым, то есть выражаться числом.
2.Значение интегрального критерия должно уменьшаться с уменьшением любого из рассмотренных показателей качества.
Рассмотрим их отдельно для неколебательных и колебательных систем.
Неколебательные системы.
Для них существуют два показателя качества, и ИККР должен зависеть от них. В качестве ИККР здесь принимают площадь между кривой переходного процесса и линией установившегося режима (рис.3.28):

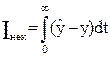 . (3.84)
. (3.84)
 |
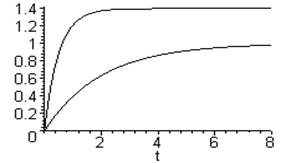
Рис. 3.28. ИККР неколебательной системы.
Колебательные системы. Применение для них вышерассмотренного критерия некорректно, так как получающиеся при интегрировании площади имеют разные знаки (рис.3.29), и общий результат неинформативен. Для этих систем часто применяют квадратичный интегральный критерий:
Iкол  . (3.85)
. (3.85)
 |
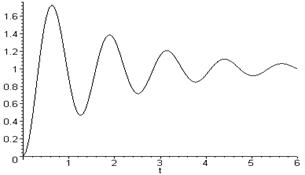
Рис.3.29. Колебательная САР.
Нередко применяются улучшенные интегральные оценки, одна из которых, например, учитывает дополнительно скорость изменения регулируемой величины:
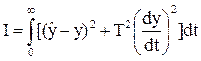 . (3.86)
. (3.86)
Чем меньше значение интегрального критерия, тем лучше система. Разумеется, при оценке пригодности того или иного регулятора к регулированию конкретного технологического процесса необходимо учитывать требования к точности управления регулируемыми величинами данного конкретного объекта регулирования.
Приближенная оценка времени переходного процесса по корням характеристического уравнения.
Если корни известны, то можно следующим образом выполнить такую оценку. Как известно, решение ДУ САР имеет вид
у=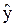 +C1exp(p1t)+ C2exp(p2t)+…+ Cnexp(pnt),
+C1exp(p1t)+ C2exp(p2t)+…+ Cnexp(pnt),
где р1, р2, … рn – корни характеристического уравнения. Время переходного процесса определяется тем, как быстро стремится к нулю общее решение, то есть члены вида Ckexp(рkt). Скорость приближения к нулю каждого из них зависит от вещественной части соответствующего корня. Если рассмотреть характеристическое уравнение системы первого порядка (например, объекта регулирования), имеющего единственный вещественный корень
Тр + 1 = 0; р = - a = - 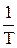 ,
,
для которого, как известно, tпп =3Т, то очевидно что 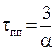 . Чем больше вещественная часть корня по абсолютной величине, тем быстрее затухает (стремится к нулю) соответствующее слагаемое. Таким образом, время переходного процесса приближенно можно оценить по формуле
. Чем больше вещественная часть корня по абсолютной величине, тем быстрее затухает (стремится к нулю) соответствующее слагаемое. Таким образом, время переходного процесса приближенно можно оценить по формуле
tпп = 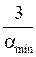 , (3.87)
, (3.87)
где amin – наименьшее значение вещественной части корня по модулю.
3.7. Взаимодействие объекта и регулятора.
Законы регулирования
В этой части будут рассмотрены поведение неавтоматизированного объекта и объекта с различными типами регуляторов при действии одинаковых возмущений, а также будет проведен сравнительный анализ качества регулирования различных вариантов. Математическое описание регуляторов будем принимать простейшее из соответствующего класса, поскольку здесь нас интересуют в большей степени принципиальные различия, чем численные значения показателей. Будем рассматривать САР, работающую по принципу обратной связи.
Дифференциальное уравнение объекта регулирования:
(Tp +1)y = kxx +kzz, (3.88)
где z рассматривается как обобщённое внешнее возмущение. Знак при возмущении примем плюс для удобства дальнейшего анализа. Итак, если нет регулятора, то нет регулирующего воздействия, и в этом случае поведение изолированного объекта описывается уравнением
(Tp +1)y = kzz. (3.89)
В разделе «объект регулирования» рассмотрено поведение объекта при действии х. При действии z = z0 аналогично имеем следующие показатели качества регулирования для объекта без регулятора (переходный процесс – неколебательный):
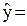 kzz0 ; tпп = 3Т,
kzz0 ; tпп = 3Т,
где z0 – величина скачкообразного возмущения.
Система «объект – регулятор».
1.Пропорциональный, или П-регулятор. САР описывается двумя уравнениями, первое из которых – уравнение объекта, второе – уравнение регулятора:
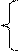 |
(Tp +1)y = kxx +kzz (3.90)
х = - kpy.
Коэффициент kp в уравнении регулятора называется коэффициентом усиления регулятора, он может быть изменён по желанию человека, и такая процедура называется настройкой регулятора. Знак минус в уравнении регулятора соответствует тому, что главная обратная связь отрицательна, это обсуждалось в теме «передаточная функция».
Исключив из этой системы х, получим уравнение САР:
[Tp + (1+kxkp)]y = kzz.
Разделив на (1+kxkp), получим
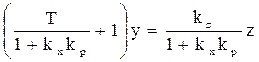 . (3.91)
. (3.91)
Уравнение (3.91) по виду аналогично (3.89), поэтому о качестве регулирования САР с П-регулятором можно сказать следующее:
- переходный процесс неколебательный;
- установившаяся ошибка и время переходного процесса в САР
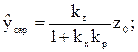


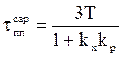 (3.92)
(3.92)
меньше, чем у объекта без регулятора (рис.3.30).
 |
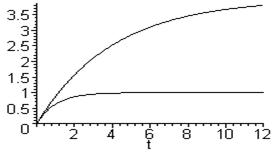
Рис.3.30. Эффект введения П-регулятора.
Увеличением коэффициента усиления регулятора достигают уменьшения обоих показателей качества. Логично возникает вопрос: возможно ли настроить регулятор на столь высокую точность регулирования, чтобы установившаяся ошибка была равна нулю? Как следует из (3.92), для этого коэффициент усиления регулятора должен быть бесконечно большим. Регуляторов с таким свойством не существует хотя бы потому, что для этого требуется бесконечно большая мощность.
Применением П-регулятора невозможно полное устранение установившейся ошибки регулирования. Практически часто обеспечивается достаточно малая ошибка, например, при регулировании частоты электроэнергии, вырабатываемой судовыми генераторами (степень неравномерности 1- 2%).
2.Интегральный, или И-регулятор. Уравнения системы:
 (Tp +1)y = kxx + kzz (3.93)
(Tp +1)y = kxx + kzz (3.93)
рх = - kiy.
Исключая из этих уравнений x = - kiy/p, после освобождения от знаменателя получим уравнение САР:
(Tp2 + p + kxki)y = kzpz. (3.94)
Уже по уравнению регулятора видно, что установившаяся ошибка в системе равна нулю. Действительно, установившийся режим наступит, когда прекратится изменение регулирующего воздействия: x = const., тогда производная px = dx/dt = 0, следовательно, 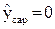 . Это можно объяснить и по уравнению САР. В его правой части имеется выражение pz= dz/dt, что при возмущении z0 = const. даёт pz0 = 0, что формально можно трактовать как исчезновение возмущения, то есть опять-таки
. Это можно объяснить и по уравнению САР. В его правой части имеется выражение pz= dz/dt, что при возмущении z0 = const. даёт pz0 = 0, что формально можно трактовать как исчезновение возмущения, то есть опять-таки 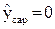 .Регулятор является астатическим, то есть на всех установившихся режимах он поддерживает одно и то же значение регулируемой величины. Такимобразом, признаком того, что установившаяся ошибка САР равна нулю, является наличие свободного оператора дифференцирования р в левой части уравнения регулятора либо в правой части уравнения САР.
.Регулятор является астатическим, то есть на всех установившихся режимах он поддерживает одно и то же значение регулируемой величины. Такимобразом, признаком того, что установившаяся ошибка САР равна нулю, является наличие свободного оператора дифференцирования р в левой части уравнения регулятора либо в правой части уравнения САР.
Недостатки интегрального регулятора. Дифференциальное уравнение САР оказалось второго порядка, и в системе возможны колебательные переходные процессы. При выполнении условия 1 - 4Tkxki < 0 корни характеристического уравнения Tp2 + p + kxki =0 комплексные вида
р1,2 = - a ± iw,
причём a = 1/2Т. Отсюда продолжительность переходного процесса
tпп = 3/a = 6Т,
то есть больше чем у объекта без регулятора (рис.3.31,а). Если же настройкой коэффициента усиления ki добиться, чтобы корни были вещественными, то один из них по модулю будет меньше 1/2Т, а значит, в этом случае продолжительность переходного процесса, определяемая, как указано в (3.87), будет больше 6Т (рис. 3.31,б).
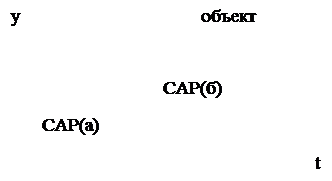 |
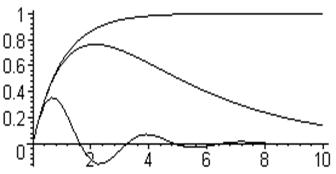
Рис.3.31. Эффекты введения И-регулятора.
3.Пропорционально-интегральный, или ПИ-регулятор. Уравнения системы:
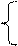 (Tp +1)y = kxx +kzz (3.95)
(Tp +1)y = kxx +kzz (3.95)
рх = - kppy - kiy.
Здесь настроечных параметров два: коэффициенты усиления пропорциональной составляющей kp и интегральной составляющей ki. Если предположить, что kp= 0, то имеем случай И-регулятора, если же ki=0, то после сокращения на р получаем П-регулятор. Поступив уже знакомым образом, приходим к уравнению САР:
[Tp2 + (1+k x kp)p + kxki]y = kzpz. (3.96)
По аналогии с И-регулятором (свободный оператор р в правой части уравнения САР) установившаяся ошибка регулирования равна нулю. Отсюда вывод: полное устранение установившейся ошибки регулирования возможно с помощью любого регулятора, имеющего интегральную составляющую в законе регулирования. Далее, характеристическое уравнение
Tp2 + (1+k x kp)p + kxki = 0
имеет корни
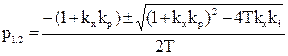 .
.
Выбрав коэффициенты настройки так, чтобы подкоренное выражение было близким к нулю и положительным, получим два вещественных, близких по модулю корня, то есть обеспечим неколебательный переходный процесс. Выбрав, кроме того, kp достаточно большим, получим два корня, больших по модулю, что обеспечивает малую продолжительность переходного процесса (рис.3.32).
 |
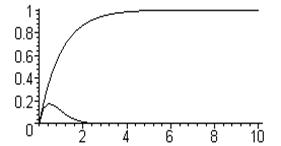
Рис.3.32. Эффект введения ПИ-регулятора.
Как видно, применение ПИ-регулятора позволяет получить весьма высокое качество регулирования.
Законы регулирования.
Законом регулирования называется выраженная в интегральной форме функциональная зависимость регулирующего воздействия (выходной величины регулятора) от регулируемой величины (входной величины регулятора). Законы регулирования имеют вид:
- для П- регулятора: x = - kpy;
- для И- регулятора: x=-ki ∫ ydt;
- для ПИ- регулятора: x = - kpy -ki ∫ ydt.
Наиболее общим законом регулирования является закон ПИД – пропорционально-интегрально-дифференциальный:
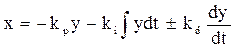 , (3.97)
, (3.97)
где присутствует производная регулируемой величины и ещё один параметр настройки – коэффициент усиления дифференциальной составляющей kd. Использование сигнала по производной позволяет во многих случаях значительно повысить точность регулирования в отношении многих показателей качества. Дифференциальное уравнение ПИД- регулятора таково:
рх = - kppy - kiy ± kdp2y. (3.98)
Обратим внимание на то, что введение в закон регулирования дифференциальной составляющей требует внимательного обращения с её знаком. При неправильно выбранном знаке дифференциальной составляющей качество регулирования может, наоборот, ухудшиться, нередко вплоть до потери устойчивости. Из ПИД-регулятора как варианты получаются П-, И-, Д-, ПИ-, ПД-, ИД, наконец, ПИД-регуляторы. Следует отметить, что самостоятельно Д-регулятор не применяется, поскольку он реагирует на скорость изменения регулируемой величины и не уменьшает статическую ошибку регулирования.
Случай неправильного включения регулятора.
На практике, к сожалению, такие случаи встречаются. Один из примеров – ошибка при подключении электропитания трёхфазного электродвигателя, используемого в САР в качестве исполнительного механизма. Не вдаваясь в рассуждения об очевидных катастрофических последствиях, рассмотрим математическую сторону вопроса на примере системы с простейшим пропорциональным регулятором.
Система уравнений САР:
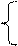 (Tp +1)y = kxx + kzz (3.99)
(Tp +1)y = kxx + kzz (3.99)
х = + kpy.
Неправильное включение подчеркнуто изменением знака в уравнении регулятора (положительная главная обратная связь). К уравнению системы придём, заменив знак при kp в выражении (91):
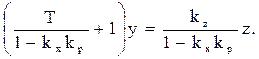
Рассмотрим характеристическое уравнение системы
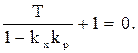
Обычно для обеспечения малой установившейся ошибки коэффициент усиления регулятора устанавливают настолько большим, что
1 - kxkp< 0,
это означает, что коэффициенты характеристического уравнения имеют разные знаки, следовательно, САР неустойчива (рис.3.33).
 |
Рис.3.33. Последствия неправильного включения регулятора.
3.8. Противоречие между статической точностью регулирования и
устойчивостью.
Рассмотрим систему стабилизации частоты вращения вала двигателя с центробежным регулятором прямого действия, имеющую следующее математическое описание:
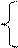 |
(Tp + 1)y = kxx - kzz
(T22p2 + T1p + 1)x = -kpy. (3.100)
Исключив из этой системы уравнений х, получим ДУ САР:
[(Tp+1)(T22p2+T1p+1)+kxkp]y = -kz(T22p2+T1p+1)z,
или, после преобразований,
[TT22p3+(TT1+T22)p2+(T+T1)p+(1+kxkp)]y = -kz(T22p2+T1p+1)z. (3.101)
Условие установившегося режима при возмущении z=z0 получим, потребовав, чтобы р =0:
(1+kxkp)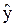 = -kzz0,
= -kzz0,
откуда
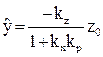 . (3.102)
. (3.102)
Очевидно, что для уменьшения статической ошибки по модулю следует увеличивать коэффициент усиления регулятора kp.
Рассмотрим характеристическое уравнение САР
TT22p3+(TT1+T22)p2+(T+T1)p+(1+kxkp)=0.
Условие устойчивости имеет вид
(TT1+T22)(T+T1) > TT22 (1+kxkp),
откуда
kp < 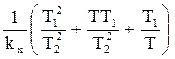 . (3.103)
. (3.103)
Оказывается, что, с одной стороны, согласно (3.102) коэффициент усиления регулятора нужно увеличивать, а с другой стороны, по условиям устойчивости (3.103) он ограничен сверху. Очевидно, что условие устойчивости накладывает ограничение снизу на величину статической ошибки.
Покажем, что описанное ограничение распространяется на системы любого порядка. Пусть собственный оператор САР имеет вид
D(p) = anpn + an-1pn-1 +…+ a1p + a0.
Как следует из предыдущих рассуждений, коэффициент a0 = 1+kxkp. Применив критерий Михайлова, получим выражения для компонент вектора кривой Михайлова:
U = a0 – a2w2 + a4w4 – a6w6 +…
V = a1w - a2w3 + a5w5 –a7w7 +…
Предположим, что система при некотором значении а0 была устойчивой (рис.3.34,кривая а). Очевидно, что при увеличении kp увеличивается а0, и кривая Михайлова смещается вправо, так что при некотором достаточно большом а0 она не пройдёт через вторую либо третью четверти (рис.3.34,кривая б), а это означает потерю устойчивости системой.
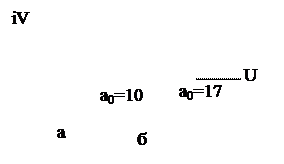 |
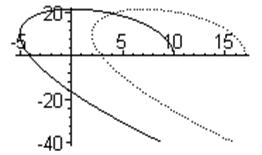
Рис.3.34. Потеря устойчивости при слишком больших
коэффициентах усиления регулятора.
4. НЕЛИНЕЙНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ
Как было сказано раньше, линейные САР описываются линейными ДУ вида
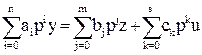 ,
,
то есть в таких системах функции и их производные входят линейно. Нелинейные САР - это такие, которые описываются нелинейными дифференциальными уравнениями, например,
p2y + (py)3 + y*py + F(y) = z. (4.1)
В уравнении (4.1) подчеркнуты признаки нелинейности, достаточно одного, чтобы САР являлась нелинейной. Если САР содержит хотя бы один нелинейный элемент, она нелинейна. Наиболее часто нелинейность обусловлена наличием нелинейных функций F(y), которые называются типовыми нелинейными характеристиками.
4.1. Типовые нелинейные характеристики и их
влияние на качество регулирования.
1.Зона нечувствительности (рис.4.1).
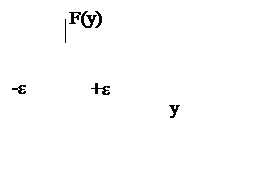 |
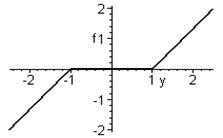
Рис.4.1. Нелинейность типа зоны нечувствительности.
y < -e Þ F(y) = k(y+e);
-e £ y £ +e Þ F(y) = 0;
y> + e Þ F(y) = k(y-e).
Диапазон (-e, +e) называется зоной нечувствительности (или мёртвой зоной), а величина e -порогом срабатывания. Такая нелинейность часто свойственна чувствительным элементам. Влияние её на качество регулирования можно проследить, рассмотрев соответствующие статические характеристики САР (рис.4.2).
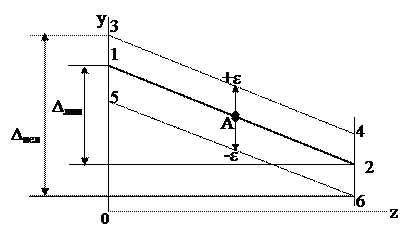 |
 2014-02-02
2014-02-02 1691
1691