Часть 1. Основы векторной алгебры
Аналитической геометрии на плоскости
Основы векторной алгебры и
Лекция № 2
Скалярным произведением двух векторов 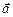 и
и 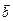 называется число, равное произведению модулей векторов на косинус угла между ними
называется число, равное произведению модулей векторов на косинус угла между ними 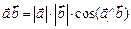 .
.
Обозначается скалярное произведение также 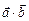 или
или 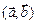 .
.
Свойства скалярного произведения:
1) Так как, в силу свойств проекции вектора, 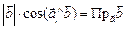 , то
, то 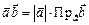 или
или 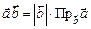 ;
;
2)  ;
;
3) 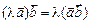 ;
;
4) 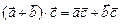 ;
;
5) Скалярное произведение вектора на себя 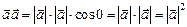
называется скалярным квадратом 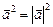 ;
;
6) Теорема 1. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы перпендикулярны
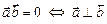 .
.
Пример 1.1. Для двух векторов 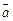 и
и 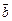 дано
дано 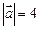 ,
, 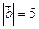 ,
, 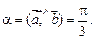
Найти 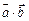 ,
, 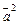 ,
, 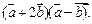
Решение. По определению скалярного произведения векторов имеем
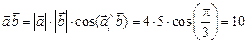 ,
,
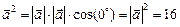 .
.
Используя свойства скалярного произведения, получим
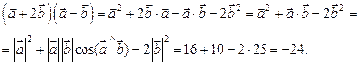
 2014-02-13
2014-02-13 555
555







