1. y = ex.
Имеем f(x) = f'(x) = f''(x) =…= f(n)(x) = ex;
f (0) = f' (0) = f'' (0) =…= f(n) (0) = e 0 = 1.
По формуле
ex = 1 + х + 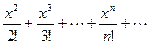 .
.
Область сходимости ряда (-∞; ∞).
2. y = sin x.
Имеем f(x) = sin x, f'(x) = cos x, f''(x) = -sin x; f'''(x) = -cos x, f(4)(x) = sin x,
откуда f (0) = 0; f' (0) = 1; f'' (0) = 0; f''' (0) = -1, f(4)( 0) = 0 и т.д.
Очевидно, что производные чётного порядка f(2n) (0) = 0, а нечётного порядка f(2n-1) (0) = (-1) n -1, i = 1, 2…. По формуле
sin x = x - 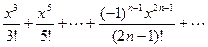 .
.
Область сходимости ряда (-∞; ∞).
3. y = cos x.
Рассматривая аналогично, получим
сos x = 1 - 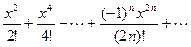 .
.
Область сходимости ряда (-∞; ∞).
4. y = (1+ x) m, где m - любое действительное число.
Имеем f(x) = (1+ x) m, f'(x) = m (1+ x) m -1, f''(x) = m (m -1) (1+ x) m -2, f'''(x) = m (m -1) (m -2) (1+ x) m -3, …., f(n)(x) = m (m -1)…(m-n +1) (1+ x) m-n.
При x = 0 f (0) = 1, f' (0) = m, f'' (0) = m (m -1), f''' (0) = m (m -1) (m -2),…, f(n) (0) = m (m -1)…(m-n +1).
По формуле
(1+ x) m = 1 + mx + 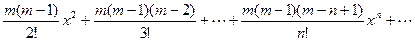 .
.
Интервала сходимости ряда (-1; 1).
Ряд называется биномиальным. Если m - целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при n = m +1 m-n +1 = 0, n -й член ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.
5. y = ln(1+ x).
Рассмотрим геометрический ряд
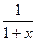 = 1 - x + x2 - x3 +…+(-1) n xn +…
= 1 - x + x2 - x3 +…+(-1) n xn +…
со знаменателем q = - х, который сходится при | q | = | - x |<1, т.е. при -1 < х < 1, к функции
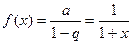 .
.
Интегрируя почленно равенство в интервале (0; х), где | x |<1, с учётом того, что
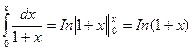 , получим
, получим
In (1+ x) = x - 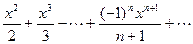 .
.
Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть 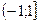 .
.
С.Р. 1.Свойства степенных рядов.
2. Формула Тейлора.
3. Применение степенных рядов.
 2014-02-09
2014-02-09 11471
11471







