Теорема о линиях элиптического типа

Теорема: Пусть задана линия элиптического типа т.е. I₂>0 и пусть I₁>0 следовательно уравнение (1) определяет: 1. I₃<0 – эллипс; 2. I₃=0 – точка; 3. I₃>0 – ур-е (1) не определяет. Если I₃=0 говорят, что эллипс вырождается в точку. Если I₃>0 говорят, что задается мнимый эллипс. Пусть после ПП и поворота ур-е (1) принимает вид (*).

Доказательство:

1. пусть I₂>0, I₁>0, I₃<0, тогда

а₁₁’’x’’²+a₂₂’’ y’’²= -I₃/I₂

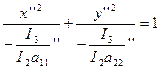
I₂=a₁₁’’a₂₂’’ > 0

I₁= a₁₁’’+a₂₂’’ > 0

a₁₁’’ > 0; a₂₂’’ > 0

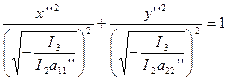
Итак, под корнями стоят положительные числа, следовательно, уравнение эллипса.

2. I₃>0 в данном случае под корнем стоят отрицательные числа, следовательно уравнение не определяет действительного геометрического образа.

3. I₃=0 в данном случае т(0,0) – случай вырождения эллипса.