Момент силы и момент импульса относительно неподвижного начала. Общефизический закон сохранения энергии

Общефизический закон сохранения энергии

Классическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннего атомистического строения вещества. При ударе, трении и аналогичных процессах кинетическая энергия видимого движения тел не пропадает. Она только переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии получила название внутренней энергии.

Беспорядочное движение атомов и молекул воспринимается нашими органами чувств в виде тепла.

Таково физическое объяснение кажущейся потери механической энергии при ударе, трении и пр.

В физике закон сохранения энергии распространяют не только на явления, рассматриваемые в механике, но на все без исключения процессы, происходящие в природе.

Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую.

В основе закона сохранения энергии лежит такое свойство времени как однородность, т.е. равнозначность всех моментов времени, заключающаяся в том, что замена момента времени t ₁ моментом времени t ₂, без изменения значений координат и скоростей тел не изменяет механических свойств системы. Поведение системы, начиная с момента времени t ₂ будет таким же, каким оно было бы, начиная с момента t ₁.

Общефизический закон сохранения энергии не может быть выведен из уравнений механики, и должен рассматриваться как одно из наиболее широких обобщений опытных фактов.

ЛЕКЦИЯ №6. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Пусть О – какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через 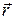радиус-вектор, проведенный из этой точки к точке приложения силы 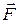(рис. 1).

Моментом силы 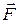относительно точки О называется векторное произведение радиуса-вектора 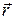на силу 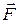: 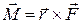, , 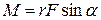(1)

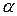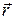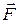– угол между векторами и ;направление 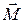выбирается так, чтобы последовательность векторов 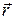, , 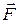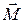образовывала правовинтовую систему, т. е. если смотреть вдоль вектора 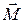, то поворот по кратчайшему пути от первого сомножителя в (1) ко второму осуществлялся по часовой стрелке, таким образом 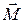совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от 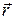к 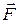по наикратчайшему пути.

Моментом 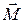нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки

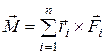. (2)

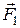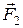Отметим частный случай двух равных параллельных сил и , направленных в противоположные стороны.

Такие силы образуют так называемую пару сил. В этом случае

,

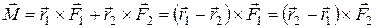т. е. момент пары сил равен моменту одной из этих сил относительно точки приложения другой.

Очевидно, что момент пары сил не зависит от выбора точки О. В частности, если равные и противоположно направленные силы 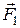и 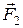действуют вдоль одной и той же прямой, то они коллинеарны с вектором 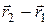, и поэтому момент пары таких сил равен нулю.

Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора 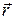на импульс :

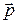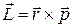. (3)

Для системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:

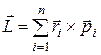. (4)