Дифференциальные уравнения поступательного,
При поступательном движении все точки тела движутся по одинаковым траекториям и в один и тот же момент времени имеют одинаковые ускорения. Тогда для описания движения можно использовать теорему о движении центра масс (67). Проектируем это уравнение на координатные оси
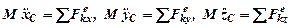 . (90)
. (90)
Система (90) представляет собой дифференциальные уравнения поступательного движения твердого тела.
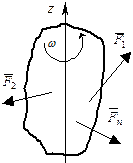 Пусть твердое тело совершает вращение относительно оси под действием сил. Динамической характеристикой вращательного движения твердого тела является кинетический момент Kz, а характеристикой вращательного действия силы - момент силы относительно оси. Поэтому для описания вращательного движения твердого тела относительно неподвижной оси воспользуемся теоремой об изменении кинетического момента (81)
Пусть твердое тело совершает вращение относительно оси под действием сил. Динамической характеристикой вращательного движения твердого тела является кинетический момент Kz, а характеристикой вращательного действия силы - момент силы относительно оси. Поэтому для описания вращательного движения твердого тела относительно неподвижной оси воспользуемся теоремой об изменении кинетического момента (81)
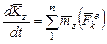 . (91)
. (91)
При вращательном движении  , тогда
, тогда
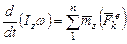 ,
,
учитывая, что Iz =const, в итоге получим
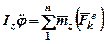 . (92)
. (92)
Уравнение (92) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.
Найденный угол j будет определять положение тела, совершающего вращательное движение, в любой момент времени.
3. Плоское движение
Положение тела, совершающего плоское движение, в любой момент времени определяется положением полюса и углом поворота тела относительно полюса. Если за полюс принять центр масс тела, то уравнение его движения можно найти по теореме о движении центра масс (67), а вращательное движение относительно центра будет определяться уравнением (92), справедливым и для движения системы относительно оси, проходящей через центр масс. Тогда дифференциальные уравнения плоского движения твердого тела имеют вид
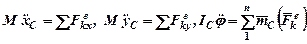 .
.
 2014-02-24
2014-02-24 2189
2189
