2014-02-24
4556
Класс вычислительных формул решения задачи Коши, основанных на квадратурных формулах численного интегрирования
Устойчивые и неустойчивые дифференциальные уравнения
Метод Эйлера решения задачи Коши. Геометрический смысл метода Эйлера
План
Лекция 34. Численные методы решения задачи Коши (продолжение)
Рассмотрим случай использования рассчетной формулы (2) предыдущей лекции, когда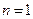 
. Тогда формула (3) предыдущей лекции примет вид:
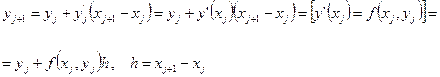(4)
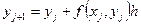
— формула Ейлера.
Геометрический смысл формулы Эйлера представлен на рисунке 1.
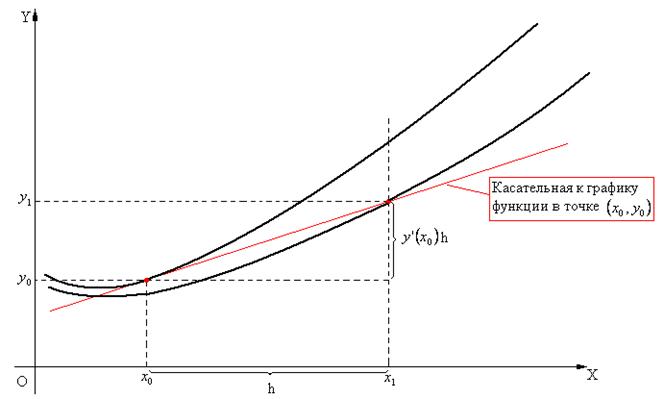
Рис.1.
В общем случае на каждом шаге приближения приближенное решение переходит на новую кривую из представленного множества решений. Для некоторых дифференционных уравнений это вызывает большие погрешности. Например, если мы имеем уравнение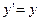 
, погрешность, которую мы имели на первых шагах приближения, будет сильно возрастать. Такое явление называется неустойчивостью дифференционного уравнения.
Рассмотрим уравнение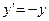 
:
, 
, 
, 
, 
.
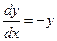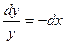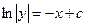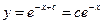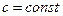Множество решений изображено на рис.2.
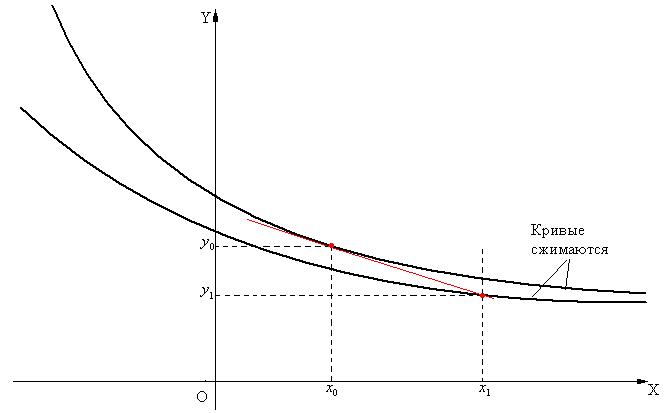
Рис.2
Погрешность, которую мы допустили сначала, будет уменьшаться. Такое явление называется устойчивостью дифференционного уравнения.
