Инверсия

Основы булевой алгебры

В цифровой технике вся имнформация представляется в двоичном виде. Теоретической основой обработки битовой информации является булева алгебра.

Аргумент булевой функции(БФ) X может быть равен 0 или 1, и булева функция Y может принимать значения 0 или 1.

X € {0, 1};

Y = f(x₁ x₂ … x_n) € {0, 1}

Для реализации основных булевых функций применяются соответствующие логические элементы.

Рассмотрим набор наиболее часто используемых булевых функций, их таблицы истинности, свойства, формулы и соответствующие им логические элементы.

y =

x y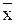

2. Логическое умножение («И», коньюнкция, AND)

y = a & b

a b y

Свойства:

1) a & 0 = 0; 2) a & 1 = a; 3) a & a &…& a = a, 4) a & 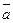= 0

3. Инверсия логического умножения («И-НЕ»)

y =

a b y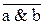

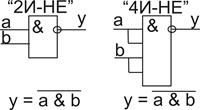
4. Логическое сложение («ИЛИ», дизъюнкция, OR)

y = a v b

a b y

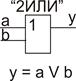
Свойства:

1) a v 0 = a; 2) a v 1 = 1; 3) a v a v…v a = a; 4) a v 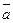= 1

5. Инверсия логического сложения («ИЛИ-НЕ», функция Пирса)

y =

a b y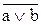

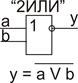
6. Функция запрет по X₁.

x1 x2 y

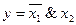
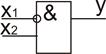
Физический (временной) смысл функции логического умножения * одновременность поступления сигналов.

7. Функция запрет по X₂.

x1 x2 y

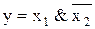
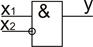
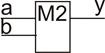
8. Функция неравнозначности (сумма по модулю 2, исключающее «ИЛИ», XOR)

a b y

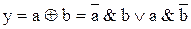
Физический (временной) смысл функции логического умножения * разновременное поступление сигналов.

Свойства:

1) a 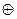0 = a; 2) a 1 = 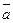; 3) a 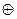a = 0; 4) a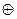 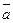= 1.