Соц адаптация

Рис.13. Барабанный парогенератор

Рис.12. Прямоточный парогенератор

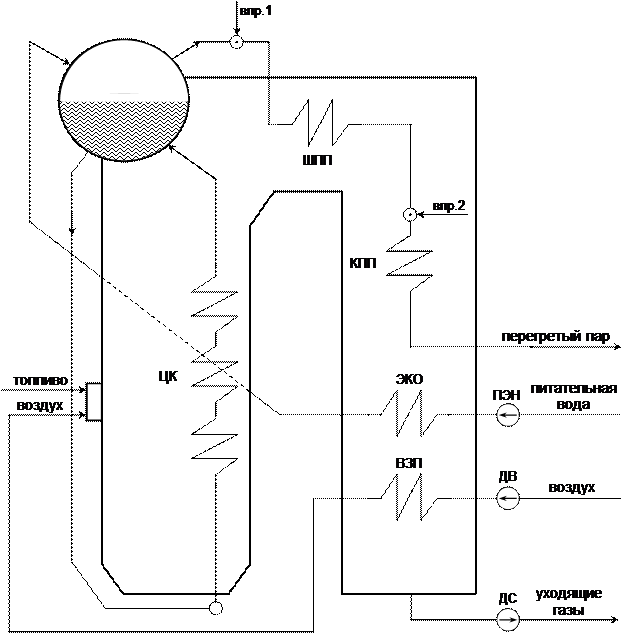
Как видно из схем, поверхности нагрева располагаются в зонах газохода с разными закономерностями теплообмена. Экранные поверхности получают теплоту в основном за счёт излучения продуктов сгорания топлива. Следовательно, интенсивность теплоподвода в этом случае практически не зависит от температуры теплоносителя (температуры поверхности нагрева). В конвективных газоходах, наоборот, интенсивность теплообмена зависит от температуры теплоносителя и тем сильнее, чем дальше по ходу газов расположена поверхность нагрева.

Внутренний теплообмен, как и внешний, сильно зависит от термодинамического состояния теплоносителя. В однофазных потоках теплообмен зависит от физических свойств и расхода теплоносителя. В области кипения интенсивность теплообмена велика, а коэффициент теплоотдачи определяется, в первую очередь, эффективностью теплосъёма с внутренней поверхности.

В парогенераторе зона с одним и тем же термодинамическим состоянием вещества может находиться в областях с разной интенсивностью обогрева или может быть выполнена в разном конструктивном исполнении. Например, парообразующая поверхность может быть выполнена в виде топочных экранов или пучка труб с конвективным теплообменом. Перегрев пара также осуществляется в поверхностях нагрева с разными способами теплоподвода.

В этих условиях представляется целесообразным рассматривать не весь парогенератор в целом, а отдельные его элементы, с тем, чтобы в последующем соединить их вместе структурной схемой. Количество элементов, на которые разбивается парогенератор, определяется его конструкцией и необходимой точностью расчёта. Обычно в качестве отдельного звена выделяют поверхности, отличающиеся своим конструктивным исполнением и термодинамическим состоянием теплоносителя. Таким образом, минимальное число элементов, на которые можно разбить парогенератор, определяется следующим набором:

§ воздухоподогреватель;

§ экономайзер;

§ радиационная парообразующая поверхность;

§ конвективная парообразующая поверхность;

§ радиационный пароперегреватель;

§ конвективный пароперегреватель.

3.2. Основные уравнения динамики парогенераторов

Процессы, протекающие в парогенераторах, описываются уравнениями неравновесной термодинамики. В неравновесной термодинамике рассматриваются системы, состоящие в общем случае из нескольких компонентов, отделённых от окружающей среды оболочкой, обладающей определёнными свойствами.

Оболочка может быть изолированной, то есть исключать переход через неё энергии и вещества, закрытой – пропускающей отдельные или все виды энергии, но не пропускающей вещество, и открытой – пропускающей как энергию, так и вещество. Свойства оболочки и процессы, протекающие на её границе, определяются взаимодействием рассматриваемой системы с окружающей средой и задаются в форме граничных условий.

Уравнения, описывающие процессы в парогенераторах, выводятся на основе законов сохранения массы, энергии, количества движения и принципов механики сплошной среды.

Математически законы сохранения можно описать дифференциальным уравнением переноса в переменных Эйлера:

,

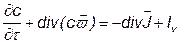состоящем из локального изменения переносимой величины 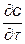, её конвективного переноса 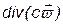, диффузионного переноса 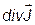и источников (стоков) величины I_v.

Уравнение закона сохранения массы (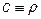) имеет следующий вид:

,

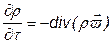где ρ – плотность; 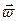– скорость центра масс элемента объёма.

Это уравнение также называют уравнением неразрывности или сплошности. В такой же форме записывается уравнение закона сохранения массы и для многокомпонентных смесей, если в них не происходит химических реакций и фазовых переходов. В противном случае в правую часть уравнения включают удельную мощность изменения массы компонента m_k, диффузионный перенос массы при этом не учитывается:

,

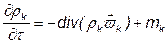где k=1,2,… – номер компонента; 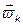и 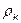– соответственно скорость и парциальная плотность компонента.

Уравнение закона сохранения количества движения (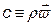, внешние силы определяются лишь гравитационным полем) имеет следующий вид:

,

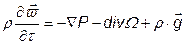где 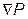– сила давления на единицу объёма; Ω – тензер вязких напряжений; 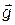– ускорение свободного падения.

Уравнение закона сохранения энергии (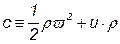) имеет следующий вид:

,

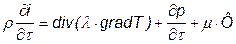где i – энтальпия; λ – коэффициент теплопроводности; Т – температура; μ – коэффициент динамической вязкости; Ф – диссипативная функция Рэлея, учитывающая рассеивание кинетической энергии вследствие действия сил вязкости.

Второй закон термодинамики характеризует возрастание энтропии в системе, в которой происходит движение вещества или энергии:

,

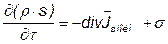где s – энтропия; 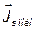– поток энтропии; σ – скорость генерирования энтропии внутренними источниками.

Скорость генерирования выражается через сумму произведений обобщённых сил X_i на обобщённые потоки J_i:

.

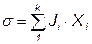Обобщённые силы, определяющие степень отклонения от термодинамического состояния равновесия, представляют собой градиенты температуры, скорости, термодинамического потенциала и т.д.

Связь между потоками и силами в первом приближении принимается линейной и задаётся в форме феноменологических законов:

.

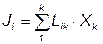Прямые коэффициенты (L₁₁, L₂₂, …, L _kk) связывают поток с прямой силой, вызывающей его, и всегда положительны. Перекрёстные коэффициенты L_ik определяют взаимное влияние одной силы на другой поток и согласно соотношению Онзагера симметричны (L_ik= L_ki).

Наиболее простыми получаются зависимости, выражающие действие лишь одной прямой силы:

.

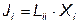К таким зависимостям, например, относятся законы Фурье и Фика:

;

,

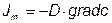где D – коэффициент диффузии; с – концентрация.

Равновесные процессы характеризуются равенством нулю скорости возникновения энтропии:

,

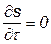а стационарные неравновесные процессы обладают свойством генерирования энтропии с минимальной скоростью.

Система уравнений законов сохранения должна быть дополнена уравнением состояния:

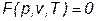
Эти уравнения совместно с граничными условиями полностью описывают поведение динамической системы в любой момент времени.

Эта адаптация ближайшему соц. окружению в коллективе, к традициям и нормам коллектива, к стилю работы руководителя. Результатом данного процесса является включение нового индивида в уже существующий коллектив, Как равноправного принимаемого всеми его членами.

Критерии эффективности:

1. Участие в общественной работе и удовлетворённость этим участием

2. Социометрический статус и удовлетворённость отношениями в коллективе

3. Отношение в целом к предприятию к коллективу, к руководителю

4. Удовлетворённость собой на работе

5. Адекватность взаимодействия с другими участниками деятельности

Степень выраженности и продолжительность адаптации определяется характеристиками индивида:

Ø Личностное различие

Ø Готовность к переменам

Ø Предшествующий опыт смены работы

Ø Наличие умений и навыков

Ø Вхождения в новую социально-проф-ую группу

В соответствии групповых отношений выделяют четыре возможных варианта последствий социального внутригруппового контакта:

1. Ассимиляция –вновь прибывшие полностью принимают те отношения, которые есть.

2. Сегрегация - отдельное развитие от группы. В конечном варианте сепаратизм.

3. Интеграция- и своё привносит и чужое принимает.

4. Геноцид- приходит новый начальник и начинает вносить сильные коррективы, работники подумывают об увольнении.