В школьном курсе алгебре и начала математического анализа в основном рассматриваются показательные неравенства вида af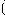 x
x
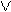 ag
ag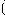 x
x , где a
, где a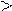 0
0 a
a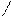 =1. При решении неравенств такого вида используется непосредственно монотонность показательной функции, учитывая область определения этой функции. Наиболее рациональное решение считается решение методом равносильных преобразований. Если в процессе решения смысл неравенства должен измениться, то символ
=1. При решении неравенств такого вида используется непосредственно монотонность показательной функции, учитывая область определения этой функции. Наиболее рациональное решение считается решение методом равносильных преобразований. Если в процессе решения смысл неравенства должен измениться, то символ 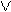 меняется на символ
меняется на символ 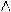 . Например,
. Например,  −x
−x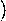
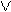 0
0 x
x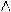 0.
0.
Равносильные преобразования показательных неравенств:
1. 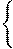 af
af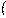 x
x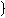
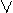 ag
ag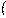 x
x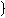 ;0
;0 a
a 1
1
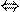 f(x)
f(x)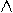 g(x).
g(x).
2. 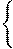 af
af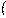 x
x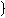
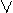 ag
ag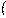 x
x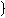 ;a
;a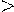 1
1
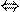 f(x)
f(x)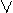 g(x).
g(x).
Замечание. Если основание показательной функции содержит переменную величину, то первое равносильное преобразование это логарифмирование обеих частей неравенства по числовому основанию большего единицы и затем использование схем равносильных преобразований логарифмических неравенств.
h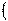 x
x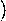 f
f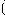 x
x
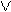 h
h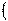 x
x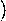 g
g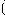 x
x
 logah
logah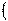 x
x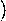 f
f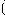 x
x
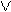 logah
logah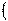 x
x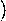 g
g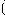 x
x
 logah
logah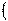 x
x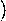
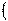 f
f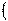 x
x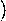 −g
−g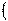 x
x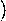
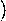
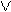 0
0
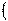 a−1
a−1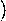
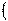 h
h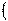 x
x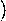 −1
−1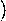
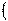 f
f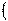 x
x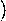 −g
−g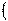 x
x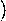
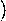
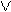 0, О.Д.З.:
0, О.Д.З.:  h
h x
x
 0;a
0;a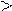 1
1 .
.
Пример. Решите неравенство x−log2x+4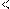 116x.
116x.
Решение: Прологарифмируем обе части по основанию 2. Тогда проделав несколько равносильных преобразований неравенство примет вид log2x−log2x+4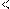 log2116x
log2116x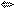
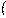 4−log2x
4−log2x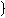 log2x
log2x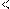 −4+log2x.
−4+log2x.
Пусть log2x=t, где x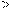 0, тогда
0, тогда 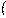 4−t
4−t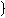 t
t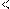 −4+t
−4+t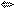
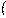 t−4
t−4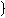
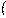 t+1
t+1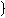
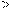 0
0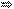 t
t
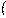 −
−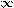 ;−1
;−1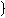
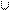
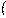 4;+
4;+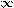
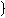 .
.
Вернемся к замене 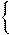 log2x
log2x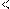 −1;log2x
−1;log2x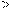 4
4
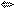
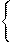 x
x
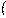 0;0
0;0 5
5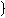 ;x
;x
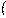 16;+
16;+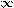
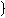
 Ответ:
Ответ: 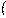 0;0
0;0 5
5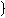
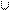
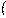 16;+
16;+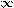
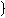 .
.
 2014-02-24
2014-02-24 922
922








