Таблица производных
Производная сложной функции
Правило вычисления производных
Если функции f и g имеют конечные производные при 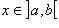 , то:
, то:
1) 
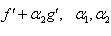 - постоянные;
- постоянные;
2) 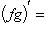
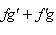 ;
;
3) 
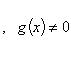 .
.
Если функции 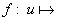
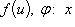
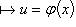 имеют конечные производные
имеют конечные производные 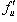 и
и 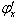 , то
, то 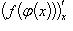
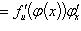 . Значком внизу обозначена переменная, по которой вычисляется производная.
. Значком внизу обозначена переменная, по которой вычисляется производная.
Если x - независимая переменная, то справедливы формулы:
1) 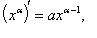
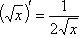 ;
;
2) (ax)' = ax ln a, a > 0, (ex)' = ex;
3) (sin x)' = cos x;
4) (cos x)' = - sin x;
5) 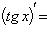
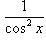 ;
;
6) 
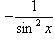 ;
;
7) 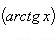
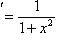 ;
;
8) 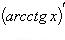
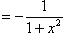 ;
;
9) 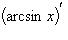
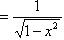 ;
;
10) 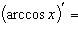
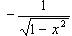 ;
;
11) 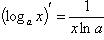
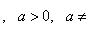
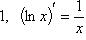 ;
;
12) (sh x)' = ch x;
13) (ch x)' = sh x;
14) 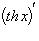
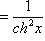 ;
;
15) 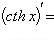
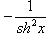 ;
;
16) 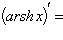
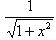 ;
;
17) 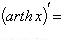
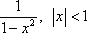 ;
;
18) 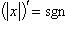
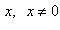 ;
;
19) 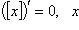
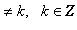 .
.
Если функции 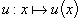 и
и 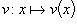 имеют конечные производные, то
имеют конечные производные, то
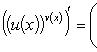
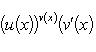
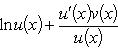
 2014-02-24
2014-02-24 1117
1117
