Обозначение предела Предел функции обозначается как 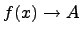 , при
, при 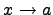 или через символ предела
или через символ предела 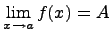 .
.
Всюду ниже предполагается, что пределы функций существуют.
Рассмотрим основные свойства пределов.
- Предел суммы
Предел суммы равен сумме пределов, если каждый из них существует, т.е.
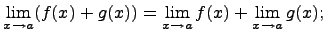
- Предел разности
Предел разности равен разности пределов, если каждый из них существует, т.е.
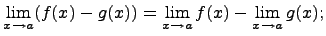
- Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
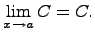
- Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
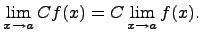
- Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.
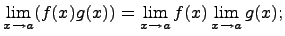
- Предел частного
Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.
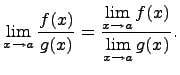
- Предел степенной функции
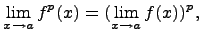
где степень p - действительное число.
- Предел показательной функции
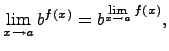
где основание b > 0.
- Предел логарифмической функции
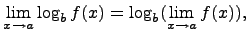
где основание b > 0.
- Теорема "о двух милиционерах"
Предположим, что 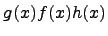 для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если
для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если
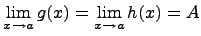
то
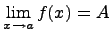
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.
Вычислить пределы: а) 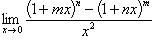 ; б)
; б) 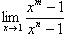 ; в)
; в) 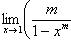
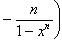 (m, n - натуральные числа).
(m, n - натуральные числа).
Решение.
а) Разлагая по формуле бинома Ньютона, получаем
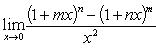
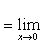
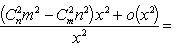
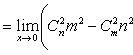
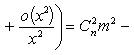
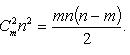
б) Полагая x = 1 + t (t → 0 при x → 1) и пользуясь принципом отбрасывания бесконечно малых, находим
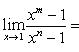
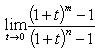
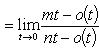
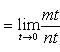
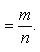
в) Пусть x = 1 + t. Тогда t → 0 при x → 1. Имеем
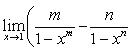
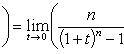
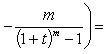
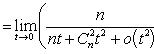
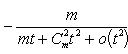
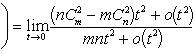
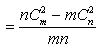
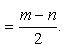
 2014-02-24
2014-02-24 11216
11216
