Вероятность достоверного события 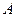 равна единице, т. к.
равна единице, т. к.
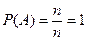 ;
;
Вероятность невозможного события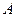 равна нулю, т. к.
равна нулю, т. к.
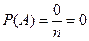 ;
;
Вероятность случайного события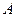 есть положительное число, заключенное между нулем и единицей, т. к.
есть положительное число, заключенное между нулем и единицей, т. к.
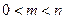 , то
, то 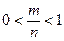 .
.
Недостатки классического определения.
1. Определение не применимо, если число элементарных исходов испытания бесконечно.
2. Часто не возможно представить результат испытания в виде совокупности элементарных событий.
3. Трудно указать основания, позволяющие считать события равновозможными. О равновозможности исходов опыта заключают из соображений симметрии.
Для преодоления 3 недостатка вводятся статистические вероятности, а для преодоления 1 недостатка – геометрические (вероятности попадания точки в область). Рассмотрим более подробно понятие статистической вероятности.
Пусть произошло 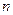 испытаний, причем в этих испытаниях событие
испытаний, причем в этих испытаниях событие 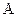 появилось
появилось  раз. Число
раз. Число  называют абсолютной частотой события
называют абсолютной частотой события 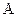 .
.
О. 3. Относительной частотой 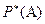 события
события 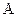 называется отношение числа испытаний, в которых событие
называется отношение числа испытаний, в которых событие 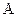 появилось к общему числу проведенных испытаний
появилось к общему числу проведенных испытаний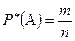 , где
, где 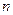 - общее число испытаний,
- общее число испытаний,  - число появлений события
- число появлений события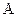 .
.
Пример 2. Среди 1000 новорожденных оказалось 515. Чему равна частота рождения мальчиков.
Событие 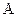 - родился мальчик. Относительная частота события
- родился мальчик. Относительная частота события 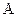 :
:
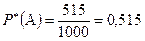
Вероятность события может быть посчитана без проведения испытания, а относительная частота считается только в том случае, если испытание проведено фактически.
Если в одинаковых условиях проводят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает следующее свойство: в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа.
О. 4. (статистическое определение) Вероятностью события 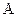 в данном испытании называется число
в данном испытании называется число 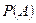 , около которого группируется значения относительной частоты
, около которого группируется значения относительной частоты 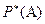 при больших
при больших 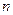
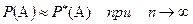 .
.
 2014-02-09
2014-02-09 807
807








