Уравнение теплопроводности для нестационарного случая
Распределение тепла в теле называют нестационарным, если температура тела зависит как от положения точки, так и от времени.
Обозначим через и = и (М, t) температуру в точке М однородного тела, ограниченного поверхностью S, в момент времени t. Известно, что количество теплоты dQ, поглощаемой за время dt, выражается равенством
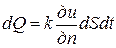 , (1)
, (1)
где dS − элемент поверхности, k − коэффициент внутренней теплопроводности, 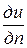 − производная функции и по направлению внешней нормали к поверхности S. Так как распространяется в направлении понижения температуры, то dQ > 0, если
− производная функции и по направлению внешней нормали к поверхности S. Так как распространяется в направлении понижения температуры, то dQ > 0, если 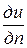 > 0, и dQ < 0, если
> 0, и dQ < 0, если 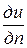 < 0.
< 0.
Из равенства (1) следует
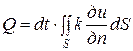 .
.
Теперь найдем Q другим способом. Выделим элемент dV объема V, ограниченного поверхностью S. Количество теплоты dQ, получаемой элементом dV за время dt, пропорционально повышению температуры в этом элементе и массе самого элемента, т.е.
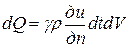 , (2)
, (2)
где 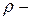 плотность вещества,
плотность вещества, 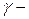 коэффициент пропорциональности, называемый теплоемкостью вещества.
коэффициент пропорциональности, называемый теплоемкостью вещества.
Из равенства (2) следует
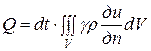 .
.
Таким образом,
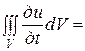
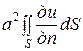 ,
,
где 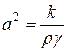 . Учитывая, что
. Учитывая, что 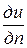 =
= 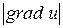 ,
, 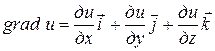 , получим
, получим
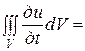
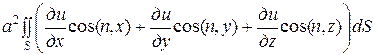 .
.
Заменяя правую часть равенства с помощью формулы Остроградского – Грина, получим
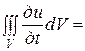
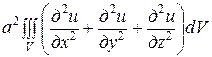
или
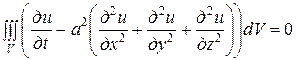
для любого объема V. Отсюда получаем дифференциальное уравнение
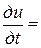
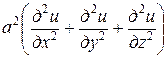 ,
,
которое называют уравнением теплопроводности для нестационарного случая.
Если тело есть стержень, направленный по оси Ох, то уравнение теплопроводности имеет вид
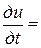
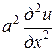 . (3)
. (3)
Рассмотрим задачу Коши для следующих случаев.
1. Случай неограниченного стержня. Найти решение 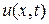 уравнения (3) (t > 0,
уравнения (3) (t > 0, 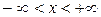 ), удовлетворяющее начальному условию
), удовлетворяющее начальному условию 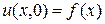 . Используя метод Фурье, получим решение в виде
. Используя метод Фурье, получим решение в виде
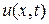 =
= 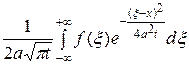
− интеграл Пуассона.
2. Случай стержня, ограниченного с одной стороны. Решение уравнения (3), удовлетворяющее начальному условию 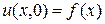 и краевому условию
и краевому условию 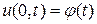 , выражается формулой
, выражается формулой
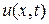 =
= 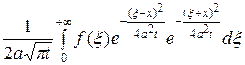 +
+ 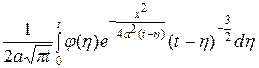 .
.
3. Случай стержня, ограниченного с двух сторон. Задача Коши состоит, чтобы при х = 0 и х = l найти решение уравнения (3), удовлетворяющее начальному условию 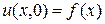 и двум краевым условиям, например,
и двум краевым условиям, например, 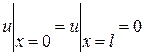 или
или 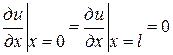 .
.
В этом случае частное решение ищется в виде ряда
 ,
,
где
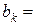
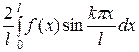
для краевых условий 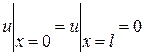 ,
,
и в виде ряда
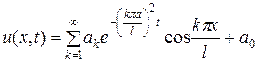 ,
,
где
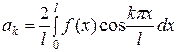 ,
, 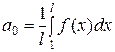
для краевых условий 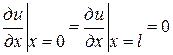 .
.
Пример. Найти решение уравнения
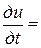
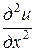
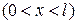 ,
, 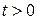 ,
,
удовлетворяющее начальным условиям
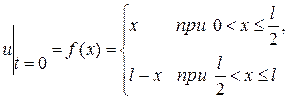
и краевым условиям 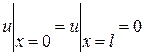 .
.
□ Решение задачи Коши будем искать в виде
 ,
,
где
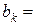
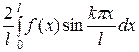 =
= 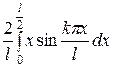 +
+ 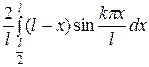 =
=
= 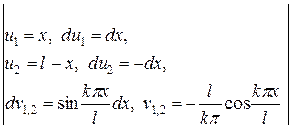 =
=  +
+
+ 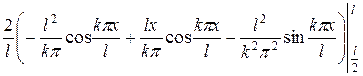 =
= 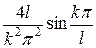 .
.
Таким образом,
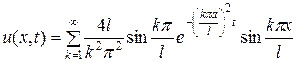
или
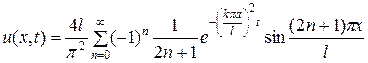 . ■
. ■
Уравнение теплопроводности для стационарного случая
Распределение тепла в теле называют стационарным, если температура тела и зависит от положения точки М (х, у, z), но не зависит от времени t, т.е.
и = и (М) = и (х, у, z).
В этом случае 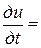 0 и уравнение теплопроводности для стационарного случая обращается в уравнение Лапласа
0 и уравнение теплопроводности для стационарного случая обращается в уравнение Лапласа
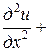
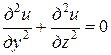 , (1)
, (1)
которое часто записывают в виде 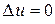 .
.
Чтобы температура и в теле определялась однозначно из этого уравнения, нужно знать температуру на поверхности S тела. Таким образом, для уравнения (1) краевая задача формулируется следующим образом.
Найти функцию и, удовлетворяющую уравнению (1) внутри объема V и принимающую в каждой точке М поверхности S заданные значения
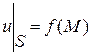 . (2)
. (2)
Эта задача называется задачей Дирихле или первой краевой задачей для уравнения (1).
Если на поверхности тела температура неизвестна, а известен тепловой поток в каждой точке поверхности, который пропорционален 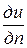 , то на поверхности S вместо краевого условия (2) будем иметь условие
, то на поверхности S вместо краевого условия (2) будем иметь условие
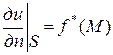 . (3)
. (3)
Задача нахождения решения уравнения (1), удовлетворяющего краевому условию (3), называется задачей Неймана или второй краевой задачей.
Для плоских фигур уравнение Лапласа записывается в виде
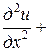
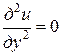 . (4)
. (4)
Такой же вид имеет уравнение Лапласа и для пространства, если и не зависит от координаты z, т.е. и (М) сохраняет постоянное значение при перемещении точки М по прямой, параллельной оси Oz.
Заменой  ,
, 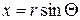 уравнение (4) можно преобразовать к полярным координатам
уравнение (4) можно преобразовать к полярным координатам
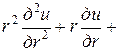
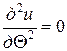 ,
,
где 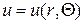 .
.
С уравнением Лапласа связано понятие гармонической функции. Функция называется гармонической в области D, если в этой области она непрерывна вместе со своими производными до второго порядка включительно и удовлетворяет уравнению Лапласа.
Пример. Найти стационарное распределение температуры в тонком стержне с теплоизолированной боковой поверхностью, если на концах стержня 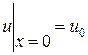 ,
, 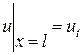 .
.
□ Имеем одномерный случай. Требуется найти функцию и, удовлетворяющую уравнению 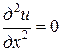 и краевым условиям
и краевым условиям 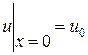 ,
, 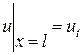 . Общее уравнение указанного уравнения имеет вид
. Общее уравнение указанного уравнения имеет вид 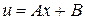 . Учитывая краевые условия, получим
. Учитывая краевые условия, получим
 .
.
Таким образом, распределение температуры в тонком стержне с теплоизолированной боковой поверхностью линейно. ■
Задача Дирихле для круга
Пусть дан круг радиуса R с центром в полюсе О полярной системы координат. Надо найти функцию 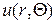 , гармоническую в круге и удовлетворяющую на его окружности условию
, гармоническую в круге и удовлетворяющую на его окружности условию 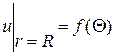 , где
, где 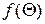 − заданная функция, непрерывная на окружности. Искомая функция должна удовлетворять в круге уравнению Лапласа
− заданная функция, непрерывная на окружности. Искомая функция должна удовлетворять в круге уравнению Лапласа
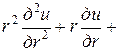
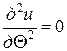 .
.
Используя метод Фурье, можно получить
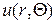 =
= 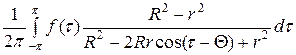
− интеграл Пуассона.
Пример. Найти стационарное распределение температуры на однородной тонкой круглой пластинке радиуса R, верхняя половина поддерживается при температуре 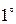 , а нижняя – при температуре
, а нижняя – при температуре 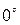 .
.
□ Если 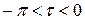 , то
, то 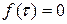 , а если
, а если 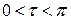 , то
, то 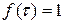 . Распределение температуры выражается интегралом
. Распределение температуры выражается интегралом
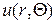 =
= 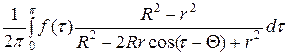 .
.
Пусть точка 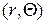 расположеиа в верхнем полукруге, т.е.
расположеиа в верхнем полукруге, т.е. 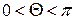 ; тогда
; тогда 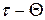 изменяется от
изменяется от 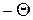 до
до 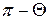 , и этот интервал длины
, и этот интервал длины 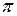 не содержит точек
не содержит точек 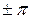 . Поэтому введем подстановку
. Поэтому введем подстановку 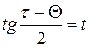 , откуда
, откуда 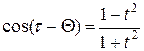 ,
, 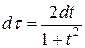 . Тогда получим
. Тогда получим
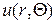 =
= 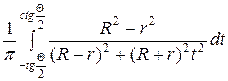 =
= 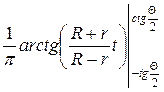 =
=
=  =
= 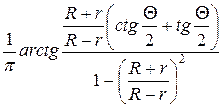 =
=
= 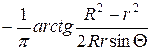
или
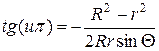 .
.
Так правая часть отрицательна, то и при 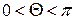 удовлетворяет неравенствам
удовлетворяет неравенствам 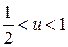 . Для этого случая получаем решение
. Для этого случая получаем решение
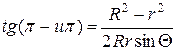 или
или 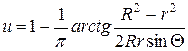 (
(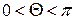 ).
).
Если же точка расположена в нижнем полукруге, т.е. 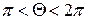 , то интервал
, то интервал 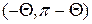 изменения
изменения 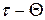 содержит точку
содержит точку  , но не содержит 0, и можно сделать подстановку
, но не содержит 0, и можно сделать подстановку 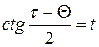 , откуда
, откуда 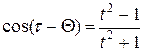 ,
, 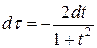 , Тогда для этих значений
, Тогда для этих значений  имеем
имеем
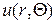 =
= 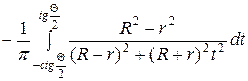 =
=
= 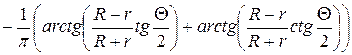 .
.
Проведя аналогичные преобразования, найдем
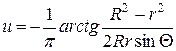 (
(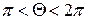 ).
).
Так как правая часть теперь положительна 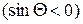 , то
, то 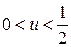 . ■
. ■
Метод конечных разностей для решения уравнения теплопроводности
Пусть требуется найти решение уравнения
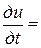
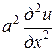 , (1)
, (1)
удовлетворяющее:
начальному условию
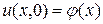 ,
, 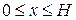 (2)
(2)
и краевым условиям
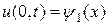 ,
, 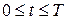 , (3)
, (3)
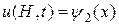 ,
, 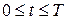 . (4)
. (4)
Итак, требуется найти решение уравнения (1), удовлетворяющее условиям (2), (3), (4), т.е. требуется найти решение 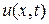 в прямоугольнике, ограниченном прямыми
в прямоугольнике, ограниченном прямыми 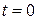 ,
, 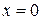 ,
, 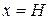 ,
, 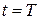 , если заданы значения искомой функции на трех его сторонах
, если заданы значения искомой функции на трех его сторонах 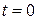 ,
, 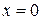 ,
, 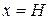 .
.
Построим прямоугольную сетку, образованную прямыми
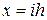
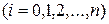 ,
,
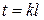
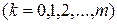 ,
,
где
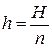 − шаг вдоль оси Ох;
− шаг вдоль оси Ох;
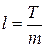 − шаг вдоль оси Оt.
− шаг вдоль оси Оt.
Введем обозначения:
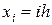 ,
,  ,
, 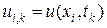 .
.
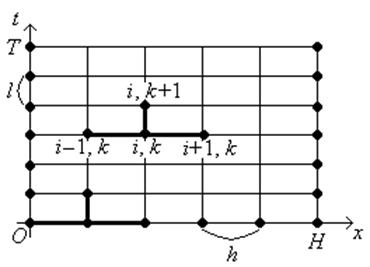
Из понятия конечных разностей можно записать
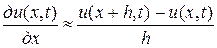 , (5)
, (5)
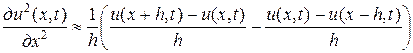
или
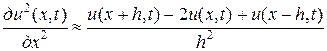 ; (6)
; (6)
аналогично
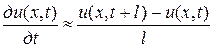 . (7)
. (7)
Учитывая формулы (6), (7) и введенные обозначения, запишем уравнение (1) в виде
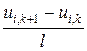 =
= 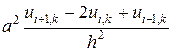 .
.
Отсюда получим расчетную формулу
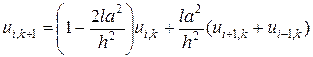 . (8)
. (8)
Из (8) следует, что если известны три значения к k -ом слое сетки: 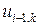 ,
, 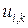 ,
, 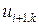 , то можно определить значение
, то можно определить значение 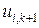 в (k + 1)-ом слое.
в (k + 1)-ом слое.
Начальное условие (2) позволяет найти все значения 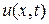 на прямой
на прямой 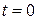 ; краевые условия (3), (4) позволяют найти значения
; краевые условия (3), (4) позволяют найти значения 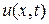 на прямых
на прямых 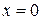 и
и 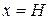 . По формуле (8) находим значения
. По формуле (8) находим значения 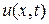 во всех внутренних точках следующего слоя, т.е. для k = 1. Значения искомой функции в крайных точках известны из граничных условий (3), (4). Переходя от одного слоя сетки к другому, определяем значения искомого решения во всех узлах сетки.
во всех внутренних точках следующего слоя, т.е. для k = 1. Значения искомой функции в крайных точках известны из граничных условий (3), (4). Переходя от одного слоя сетки к другому, определяем значения искомого решения во всех узлах сетки.
Формула (8) справедлива, если шаги 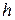 и
и 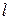 выбраны так, что выполняется неравенство
выбраны так, что выполняется неравенство
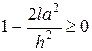 ,
,
т.е. при 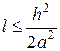 . Если
. Если 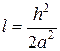 , то формула (8) значительно упрощается:
, то формула (8) значительно упрощается:
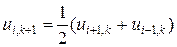 . (9)
. (9)
Замечание. При решении конкретной задачи для того, чтобы контролировать правильность хода решения и для того, чтобы нагляднее представить характер распространения тепля с стержне (либо другой физической величины, если рассматривается другой физический процесс) удобно представлять графически результаты расчета на каждом слое сетки (начать следует с графического представления начального условия).
Пример. Найти методом конечных разностей приближенное решение уравнения
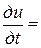
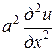 ,
,
удовлетворяющее:
начальному условию
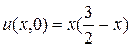 ,
, 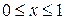 , (1)
, (1)
и краевым (граничным)условиям
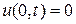 ,
, 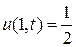 ,
, 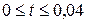 . (2)
. (2)
□ Выберем шаг по оси Ох, равным  . Шаг по оси Ot выберем, исходя из условия
. Шаг по оси Ot выберем, исходя из условия 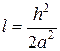 = 0,01. При таком выборе
= 0,01. При таком выборе 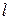 расчеты можно вести по формуле (9). Разбиваем прямоугольник, в котором разыскивается решение, линиями
расчеты можно вести по формуле (9). Разбиваем прямоугольник, в котором разыскивается решение, линиями 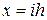
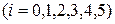 и
и 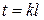
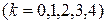 и проводим нумерацию узлов полученной сетки:
и проводим нумерацию узлов полученной сетки:
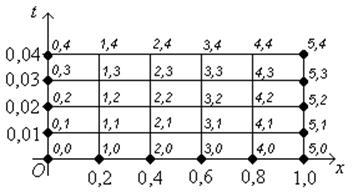
Из граничных условий (2) получаем, что в крайних левых и правых узлах сети
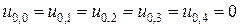 ,
,
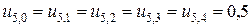 .
.
Из начального условия (1) находим значения функции 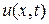 в узлах нулевого слоя:
в узлах нулевого слоя:
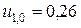 ;
; 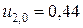 ;
; 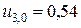 ;
; 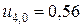 .
.
Распределение температуры при 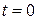 представлено на графике (рис. 1).
представлено на графике (рис. 1).
В дальнейшем расчеты ведутся по формуле (9):
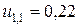 ;
; 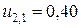 ;
; 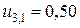 ;
; 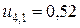 ,
,
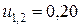 ;
; 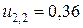 ;
; 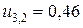 ;
; 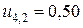 ,
,
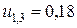 ;
; 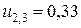 ;
; 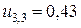 ;
; 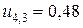 ,
,
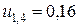 ;
; 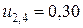 ;
; 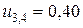 ;
; 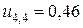 .
.
Распределение температуры при  ,
, 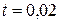 ,
, 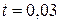 ,
, 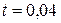 представлена на рис. 2, рис. 3, рис. 4, рис. 5 соответственно:
представлена на рис. 2, рис. 3, рис. 4, рис. 5 соответственно:
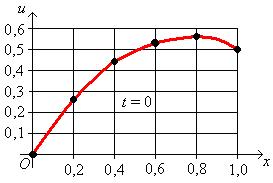
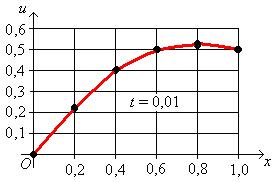
Рис. 1 Рис. 2
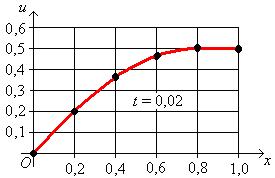

Рис. 3 Рис. 4
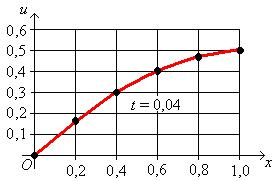
Рис. 5
■
 2014-02-09
2014-02-09 5649
5649
