Рисунок 10.3
Рисунок 10.1
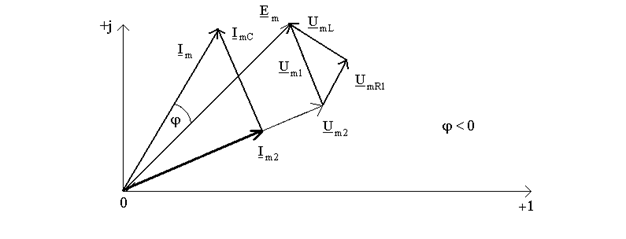
Pисунок 10.2
Рассмотренный пример можно проанализировать также с помощью векторной диаграммы (рис.10.2). Для этого необходимо задаться вектором тока (напряжения) для наиболее отдаленного участка электрической цепи, а потом провести геометрические построения на основе законов Ома и Кирхгофа. Последовательность действий может быть такой:
1) задаем вектор 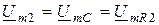 ;
;
2) строим векторы 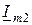 и
и 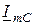 , учитывая, что первый совпадает по фазе с вектором
, учитывая, что первый совпадает по фазе с вектором 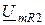 , а второй опережает вектор
, а второй опережает вектор 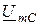 на угол
на угол 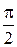 ;
;
3) вектор 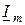 находим по первому закону Кирхгофа
находим по первому закону Кирхгофа 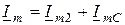 ;
;
4) зная 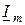 , строим вектор
, строим вектор 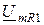 , который совпадает по фазе с
, который совпадает по фазе с 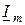 (т.е., эти векторы паралельны), и вектор
(т.е., эти векторы паралельны), и вектор 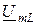 , который опережает вектор тока
, который опережает вектор тока 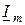 по фазе на угол
по фазе на угол 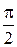 ;
;
5) по второму закону Кирхгофа: 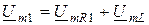 ;
; 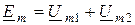 .
.
6) поскольку сдвиг фаз между вектором 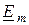 и током
и током 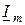
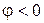 , делаем вывод, что входное сопротивление цепи имеет емкостной характер.
, делаем вывод, что входное сопротивление цепи имеет емкостной характер.
10.1 Соотношение между активнымии i реактивными составляющими
ребер и проводимостей участки цепи
Рассмотрим пассивный двуполюсник. Пусть комплексные амплитуды напряжения и тока на входе двуполюсника равняются:
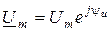 ;
; 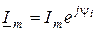
Найдем комплексное входное сопротивление:
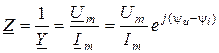
Итак, модули 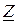 и
и 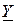 обратно пропорциональны, а аргументы противоположны:
обратно пропорциональны, а аргументы противоположны:
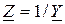 ;
; 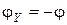 .
.
Кроме показательной формы записи 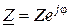 и
и 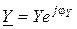 широко используется также алгебраическая форма записи этих комплексных величин:
широко используется также алгебраическая форма записи этих комплексных величин: 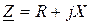 ;
; 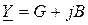 , что соответствует последовательному (R и X) и параллельному (G и B) объединению элементов двуполюсника. Установим связь между активными и реактивными составными Z и Y:
, что соответствует последовательному (R и X) и параллельному (G и B) объединению элементов двуполюсника. Установим связь между активными и реактивными составными Z и Y:
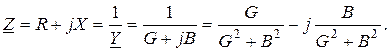
Итак,
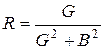 ;
; 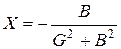 . (10.1)
. (10.1)
В свою очередь, если задано комплексное сопротивление двуполюсника Z, то комплексная проводимость
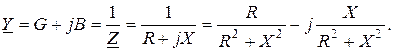
Итак,
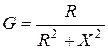
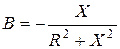 . (10.2)
. (10.2)
Вывод. Формулы (10.1), (10.2) показывают, что:
1) реактивное сопротивление X и реактивная проводимость B одном и том же участке электрической цепи имеют одинаковый характер;
2) каждая составная проводимостей(G и B) зависит как от активного, так и от реактивного ребер (R и X). Соответственно, каждая составная сопротивлению (R и X) есть функцией G и B;
3) активные составляющие R и G также зависят от частоты.
10.2 Энергетические соотношение в цепи синусоидного тока
Предположим, что через участок электрической цепи, который имеет сопротивление Z, проходит ток 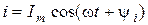 . Спад напряжения на этом ребре равняется
. Спад напряжения на этом ребре равняется 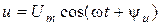 .
.
Мгновенная мощность, которая поступает в цепь, будет представлять:
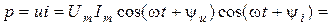
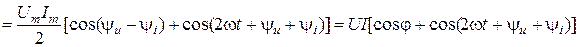 .
.
Эта мощность состоит из двух слагаемых: постоянной величины 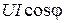 и синусоидной величины, которая имеет удвоенную частоту. Среднее значение второго слагаемого за время T равняется нулю. Поэтому активная мощность, которая поступает в рассматриваемый участок цепи, будет такой:
и синусоидной величины, которая имеет удвоенную частоту. Среднее значение второго слагаемого за время T равняется нулю. Поэтому активная мощность, которая поступает в рассматриваемый участок цепи, будет такой:
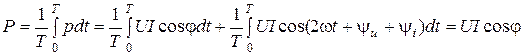 . (10.3)
. (10.3)
или
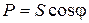 , (10.4)
, (10.4)
где 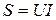 - полная мощность, которая равняется произведению действующих значений напряжения и тока, которые касаются одного и тот же входа;
- полная мощность, которая равняется произведению действующих значений напряжения и тока, которые касаются одного и тот же входа;
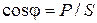 - коэффициент мощности, который равняется отношению активной мощности к полной.
- коэффициент мощности, который равняется отношению активной мощности к полной.
При расчетах электрических цепей пользуются также понятием реактивной мощности, которая исчисляется по формуле
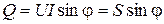 (10.5)
(10.5)
и является мерой потребления (или изготовления) реактивного тока.
Измеряется в вольт-амперах реактивных [Вар]. Реактивная мощность есть положительна при 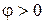 (индуктивная нагрузка) и отрицательной при
(индуктивная нагрузка) и отрицательной при 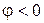 (емкостная нагрузка).
(емкостная нагрузка).
Подадим мощность в комплексной форме. Для этого перейдем от мгновенных значений напряжения и тока к комплексным амплитудам:
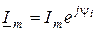 ;
; 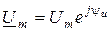 .
.
Введем понятие комплексно-сопряженных амплитудного и действующего значений тока: 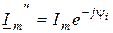 i
i 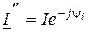 (рис.10.3а). Домножим комплексное действующее значение U на комплексно-сопряженное значение
(рис.10.3а). Домножим комплексное действующее значение U на комплексно-сопряженное значение 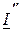 :
:
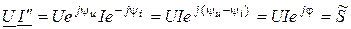 .
.
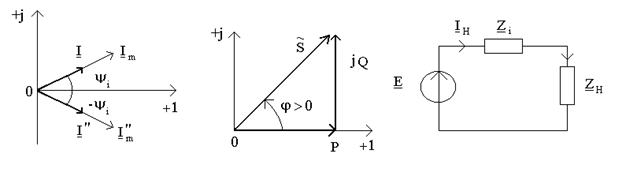
а) б) в)
Величина 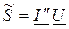 , которая равняется произведению комплексного действующего значения напряжения на комплексно-сопряженное действующее значение тока, носит название комплексной мощности. Комплексная мощность может быть записанна в показательной форме:
, которая равняется произведению комплексного действующего значения напряжения на комплексно-сопряженное действующее значение тока, носит название комплексной мощности. Комплексная мощность может быть записанна в показательной форме:
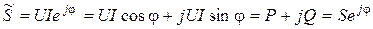 , (10.6)
, (10.6)
где P - активная мощность; Q - реактивная мощность синусоидного тока, которая равняется мнимой части комплексной мощности. Из (10.6) получается, что модуль комплексной мощности 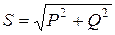 равняется полной мощности, а аргумент - сдвигу фаз между напряжением и током. На основе (10.6) можно построить треугольник мощностей (рис.10.3б). На комплексной плоскости значение
равняется полной мощности, а аргумент - сдвигу фаз между напряжением и током. На основе (10.6) можно построить треугольник мощностей (рис.10.3б). На комплексной плоскости значение 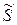 соответствует иiпотенузе прямоугольного треугольника, катетами которого есть P и Q.
соответствует иiпотенузе прямоугольного треугольника, катетами которого есть P и Q.
Найдем выражение для баланса мощностей в цепи синусоидного тока. В 6.3 было найдено условие баланса мощностей в цепи постоянного тока (6.5)-(6.6), согласно с которой алгебраическая сумма мощностей источников электрической энергии 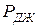 равняется сумме активных мощностей
равняется сумме активных мощностей 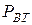 , которые тратятся в сопротивлениях:
, которые тратятся в сопротивлениях:
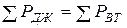 .
.
Можно показать, что в цепи синусоидного тока еще и сумма реактивных мощностей, которые поступают в цепь, равняется сумме реактивных мощностей, которые потребляются, т.е. 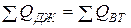 .
.
Итак, для синусоидной цепи условие баланса мощностей будет иметь вид:
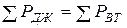 ;
; 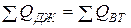 ;
; 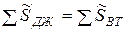 . (10.7)
. (10.7)
10.3 Условие согласования источника с нагрузкой
в цепи синусоидного тока
Пусть необходимо найти комплексное сопротивление нагрузки 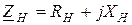 так, чтобы при заданном комплексном ребре источника
так, чтобы при заданном комплексном ребре источника 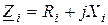 обеспечивалась передача максимума активной мощности от источника к нагрузке (рис.10.3в). Активная мощность, которая потребляется нагрузками, представляет
обеспечивалась передача максимума активной мощности от источника к нагрузке (рис.10.3в). Активная мощность, которая потребляется нагрузками, представляет 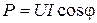 . Учитывая, что
. Учитывая, что 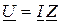 ;
; 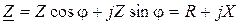 , будем иметь
, будем иметь 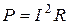 .
.
Комплексный и сопряженный ток в нагрузке будут равняться:
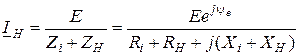 ;
; 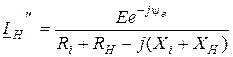 .
.
Тогда
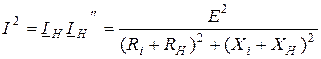 ;
; 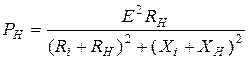 .
.
Анализируя выражение для мощности 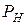 , делаем вывод, что максимальная активная мощность в нагрузке
, делаем вывод, что максимальная активная мощность в нагрузке
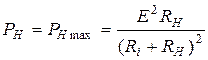
имеет место при условии 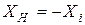 . Это первое условие согласования. В 6.3 было показано, что
. Это первое условие согласования. В 6.3 было показано, что 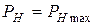 при условии
при условии 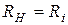 . Тогда
. Тогда 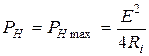 .
.
Итак, условием передачи максимальной активной мощности к нагрузке в цепи синусоидного тока есть условие:
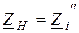 , или
, или 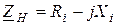 .
.
 2014-02-09
2014-02-09 528
528








