2014-02-09
746
Параметры системы автоматического управления, т.е. коэффициенты усиления и постоянные времени, зависят от физических параметров элементов, входящих в систему (сопротивления, емкости, индуктивности и т.п.). Величины этих физических параметров могут иметь разброс значений вследствие допусков на изготовление (технологический разброс), изменения параметров в процессе работы, изменения внешних условий (температуры, влажности, атмосферного давления, солнечной радиации и т.п.) Эти изменения параметров приводят к изменению статических и динамических характеристик системы.
Поэтому возникает задача определения влияния разброса и изменения параметров системы на точность системы, на её временные и частотные характеристики. Степень влияния разброса и изменения параметров системы на её статические и динамические свойства называются чувствительностью системы. В качестве оценки чувствительности используются так называемые функции чувствительности, представляющие собой частотные производные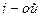 
координаты системы по вариации 
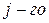параметра:
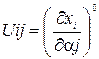
или частные производные от используемого критерия качества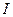 
по 
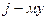параметру:
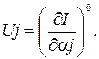
Нулевой индекс показывает, что частные производные берутся при расчетных значениях параметров.
Рассмотрим функции чувствительности временных характеристик, с помощью которых оцениваются влияние малых отклонений параметров системы от расчетных значений на временные характеристики.
Исходной системой называют систему, у которой все параметры равны расчетным значением и не имеют вариаций. Этой системе соответствует основное движение.
Варьированной системой называют такую систему, у которой произошли вариации параметров. Движение её называют варьированным движением.
Дополнительным движением называют разность между варьированным и основным движением.
Пусть исходная система описывается совокупностью нелинейных дифференциальных уравнений в форме Коши:
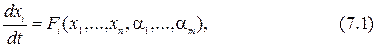
где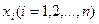 
− координаты системы. Изменяющиеся со временем параметры системы в процессе её эксплуатации обозначим через
.
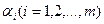Если малые изменения параметров не изменяют порядок дифференциального уравнения, то варьированное движение будет описываться совокупностью уравнений:
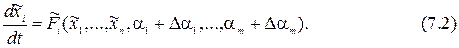
Для дополнительного движения можно записать:
При таком способе нахождения дополнительного движения возникает большая ошибка, т.к. вычитаются близкие величины. Поэтому дополнительное движение находится другим способом:
Если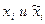 
допускают дифференцирование по 
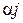, то дополнительное движение может быть разложено в ряд Тейлора. Если вариации параметров 
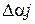малы, то можно ограничиваться линейными членами разложения. Тогда уравнение для дополнительного движения в первом приближении можно записать в виде:
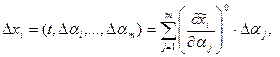
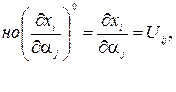
отсюда следует
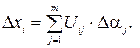
Таким образом, первое приближение для дополнительного движения может быть найдено при известных функциях чувствительности и различных вариациях параметров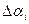 
.
Для нахождения функций чувствительности продифференцируем уравнение
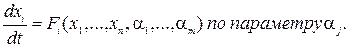
По правилу дифференцирования сложной функции имеем:
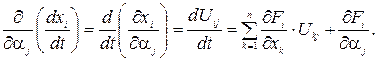
Полученные уравнения называются уравнениями чувствительности.
Решением этих уравнений является функция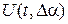 
, которая характеризует чувствительность решения исходного уравнения к изменению параметра 
.
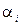Особенностью уравнений чувствительности является то, что они всегда линейны, если даже исходное уравнение было нелинейным, т.к. производные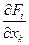 
не зависят от 
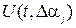. Кроме того, если исходное уравнение линейно относительно 
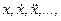то левая часть уравнения чувствительности будет иметь такую же структуру и иметь те же коэффициенты, что и исходное уравнение.
Уравнение чувствительности в общем случае аналитически решено быть не может, т.к. для этого необходимо знать решение исходного уравнения, но с помощью ЭВМ можно совместно решить исходное уравнение и уравнение чувствительности.
Пример.
Система описывается дифференциальным уравнением вида:
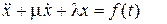(7.4)
Для определения чувствительности к отклонению параметра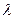 
, уравнение (7.4) продифференцируем по параметру .
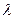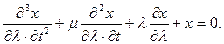
Отсюда можно записать:
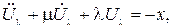(7.5)
где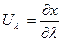 
.
Уравнение чувствительности (7.5) совпадают по структуре с уравнением (7.4), за исключением правой части. Поэтому они могут быть решены с помощью той же программы ЭВМ, которая использовалась для решения исходного дифференциального уравнения (7.4).
Для исследования чувствительности САУ разработаны методы, позволяющие строить модели чувствительности непосредственно по структурной схеме исходной системы.
