Сравнение бесконечно-малых функций.
Определение 1. 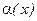 является в т.
является в т. 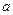 бесконечно-малой более высокого порядка, чем
бесконечно-малой более высокого порядка, чем  , если
, если 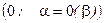
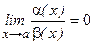
Определение 2. 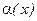 и
и  - бесконечно-малые одного порядка, если
- бесконечно-малые одного порядка, если
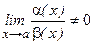 (и конечен)
(и конечен)
Определение 3. 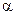 и
и 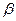 - эквивалентны, если
- эквивалентны, если 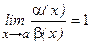
Пример. 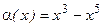
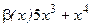 т. 0.
т. 0.
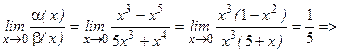 одного порядка
одного порядка
Теорема 1. (о действиях над пределами)
Пусть существует 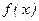 и
и 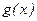 ,
, 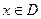 .
.

Тогда существуют пределы 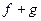 ,
, 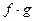 ,
, 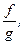
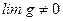 .
.
1) 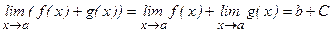
2) 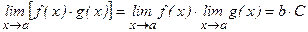
3) 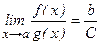
Следствия.
4) 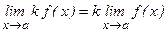
5) 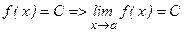
Теорема 2. (о двустороннем ограничении)
Пусть 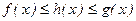 и
и 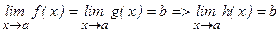
Теорема 3. (о сохранении знака)
Если существует 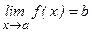 и
и 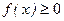 (
(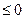 ) в
) в 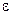 -окрестности точки а =>
-окрестности точки а => 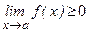 (
(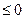 )
)
Доказательство (от противного )
Пусть 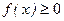 , а
, а 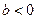 .
.
Тогда 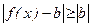 =>
=>  не меньше
не меньше 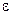 , следовательно,
, следовательно,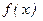 не стремиться к b
не стремиться к b
Теорема 4. (о сравнении пределов)
Если 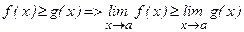
Доказательство
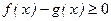
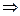 по теореме 3,
по теореме 3, 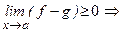
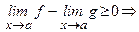
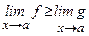
Теорема 5. Если 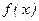 ↑(↓) и
↑(↓) и 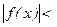 M => существует
M => существует 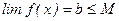
 2014-02-09
2014-02-09 384
384







